of drdr.xp Blog drdrxp @weibo.com
on algo

slimarray: gzip的压缩率, 即时访问

slimarray 是一个静态整数压缩数组, 现实数据达到和gzip相当的压缩率, 无需解压就可以直接使用. slimarray at github

场景和问题

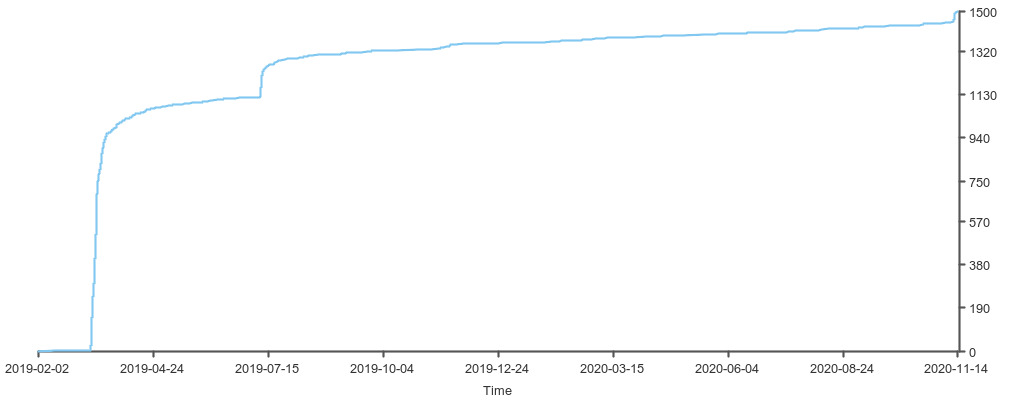
在时序数据库, 或列存储为基础的系统中, 很常见的形式就是存储一个整数数组, 例如 slim 这个项目按天统计的 star 数:

Stargazers over time

这类数据有有很明显的统一的变化趋势, 对这类数据的存储, 我们可以利用数据分布的特点, 将整体数据的大小压缩到几分之一. 这就是 slimarray 要做的事情.

使用 slimarray, 可以将数据容量减小到gzip差不多的大小, 同时还能允许直接访问这些数据! 测试中我们选择了2组随机数, 以及现实中的2份数据, 一个ipv4的数据库, 一个 slim 的star变化数据, 服用 slimarray 后效果如下:

Data size Data Set gzip size slimarry size avg size ratio
1,000 rand u32: [0, 1000] x 824 byte 6 bit/elt 18%
1,000,000 rand u32: [0, 1000,000] x 702 KB 5 bit/elt 15%
1,000,000 IPv4 DB 2 MB 2 MB 16 bit/elt 50%
600 slim star count 602 byte 832 byte 10 bit/elt 26%

在达到gzip同等压缩率的前提下, 构建 slimarray 和 访问的性能也非常高:

  • 构建 slimarray 时, 平均每秒可压缩 6百万 个数组元素;
  • 读取一个数组元素平均花费 7 ns/op.

本文手把手的介绍 slimarray 的原理, 实现:

初步想法: 前缀压缩

假设我们有一个包含4个元素的uint32的整数数组:

nums = [1006, 1005, 1007, 1010]

前缀压缩的思路就是把每个元素的公共部分提取出来单独存储, 这样每个单独元素就只需要存储它跟公共部分差异的部分, 从而大大降低存储空间. (因为公共部分在大多数情况中都在前面(例如现实中大部分被存储的数据都是排序的, 或近似于排序的), 所以一般提取公共部分的压缩都是前缀压缩)

在这个例子中, 我们看到最小的数是1005, 那么就把它作为公共部分提取出来, 再单独存储每个数字剩余的部分(和prefix的差异), 最后存储的内容如下:

{
  Prefix: 1005
  deltas: [
    1,
    0,
    2,
    5
  ]
}

可以看到这种表示方法中, 固定的部分Prefix大小不变, 影响整个存储效率的是deltas, 而它只需要记录每个原始值跟前缀之间的差, 最大是5, 也就是说每个delta 只需要3 bit就够了.

当数据较多时, 均摊空间开销将近似于3 bit/elt.

现在我们换一个视角, 我们可以把要存储的数值看做是一个坐标系中的4个点: 横轴表示数组下标, 纵轴表示数字的值.

于是前缀压缩就可以看成是: 记录一条水平直线(y = 1005), 再记录数组中实际数值跟这条直线之间的y轴方向距离:

y = 1005
num[0] = y(0) + 1 = 1006
num[1] = y(1) + 0 = 1005
num[2] = y(2) + 2 = 1007
num[3] = y(3) + 5 = 1010
                                                (3, 1010)







                                    (2, 1007)

            (0, 1006)

........................(1, 1005)...........................

🤔!!!

从坐标系这种视角, 似乎还可以进一步减小存储空间, 考虑到现实中, 一个数组中的数值, 可能是趋向于一个持续的变化(如递增的), 而不是围绕某个特定值的(如1005).

例如大家的账上余额, 应该是逐月递增的🤔.

所以, 先描述这个趋势, 再用delta数组去修正到正确值, 应该可以更大程度的降低delta的取值范围. 作者经过仔细认真的观察和研究, 突然间发现可以定义一条直线方程, 再通过delta数组去修正, 就是这个样子:

y = 1003.6 + 1.4x
num[0] = y(0) + 3 = 1006
num[1] = y(1) + 0 = 1005
num[2] = y(2) + 1 = 1007
num[3] = y(3) + 3 = 1010
                                                (3, 1010)

                                                        ....
                                                   .....
                                             ......
                                    (2, 1007)
                                  ......
            (0, 1006)       ......
                       .(1, 1005)
                 ......
            .....
      ......
......

这样描述数值趋势, delta的最大值只有3, 只需要2个bit就可以了. 于是当数据量增大时, 均摊空间效率就是 2 bit/elt.

显然, 用更高次的曲线去拟合, 可以更贴合原始点, 得到更高的压缩率. 例如使用2次曲线, 可以得到如下一份配置:

y = 1005.6 - 1.6x + x²
num[0] = y(0) + 1 = 1006
num[1] = y(1) + 0 = 1005
num[2] = y(2) + 1 = 1007
num[3] = y(3) + 1 = 1010
                                                           .
                                                          .
                                                        ..
                                                      ..
                                                     .
                                                   ..
                                                (3, 1010)
                                              ...
.                                           ..
 ..                                      ...
   ....                             (2, 1007)
       .... (0, 1006)            ....
           .............(1, 1005)

这里每个delta只需要1个bit就够了.

按照这种思路, 在给定数组中找到一条曲线来描述点的趋势, 再用一个比较小的delta数组修正曲线到实际点的距离, 得到原始值, 就可以实现大幅度的数据压缩. 而且所有的数据都无需解压全部数据就直接读取任意一个.

找到趋势函数

寻找这样一条曲线就使用线性回归, 例如在 slimarray 中使用2次曲线 f(x) = β₁ + β₂x + β₃x², 所要做的就是确定每个βᵢ的值, 以使得f(xⱼ) - yⱼ的均方差最小. xⱼ是数组下标0, 1, 2…; yⱼ是数组中每个元素的值.

\[X = \begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{bmatrix} , \vec{\beta} = \begin{bmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \\ \end{bmatrix} , Y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\]

现在要找到一组β, 使得均方差最小:

\[||X{\vec {\beta }}-Y||^{2}\]

在上面这个函数里, 把 β 看做变量, 要找极值的话就看这个函数对 β 的导数何时为0:

\[\begin{aligned} & \frac {\partial||X{\vec {\beta }}-Y||^{2}} {\partial\vec \beta } \\ = & \frac{\partial ((X \vec \beta -Y)^{T}(X{\vec {\beta }}-Y))} {\partial \vec \beta} \\ = & \frac{\partial (Y^{T}Y-Y^{T}X{\vec {\beta }}-{\vec {\beta }}^{T}X^{T}Y+{\vec {\beta }}^{T}X^{T}X{\vec {\beta }})} {\partial \vec \beta} \\ = & -2X^{T}Y+2X^{T}X{\vec {\beta }} \end{aligned}\]

于是得到 β 跟点集的关系为:

\[{\vec {\hat {\beta }}}=(X^{T}X)^{-1}X^{T}Y\]

构建slimarray, 也就是压缩数据的过程, 就是把数组下标作为向量X, 数组元素的值作为向量Y,带入到上面的式子取得β, 再逐点计算曲线到点的距离, 生成delta数组.

寻找最佳分段拟合策略

  • 但是我们看到曲线的存储也有开销, 例如y = 1005.6 - 1.6x + x² 这样一个二次曲线, 需要3个浮点数(3个64bit)来存储, 高次曲线可以获得更小的delta数组, 但本身的存储开销变大. 同时更高次的曲线, 在还原原始数组时的计算量也更高(计算开销跟曲线次数是O(n²)的关系). 在经过一些测试后, slimarray的实现中选择了二次曲线, 它在存储空间和计算性能方面的平衡最好.

  • 同时, 一条曲线也可能无法描述整个数组的趋势, 实现时需要把数组分成多段, 逐段拟合, 压缩.在我们的实现中, 将数组拆分成 每16个数字一组, 对每16个数字拟合一条曲线和对应的delta数组.

    然后再尝试将相邻的2组合并, 用一条曲线去拟合, 看最终得到的空间效率是否更低, 也就是对比3个系数+32个delta₁ 的开销 跟 6个系数+32个delta₂ 的开销. 如果相邻2组数字的趋势差不多, 那么合并之后, 可以省掉3个系数的存储空间, 而且很可能delta所需的bit宽度不会因为拟合之后变大, 那么就进一步节省了空间.

    重复这个步骤寻找可以合并的相邻的组, 最终得到这个算法下最优的配置.

实现

描述分区的数据结构: span

最后我们将整个数组划分为若干个16*k 大小的分区(span)后, 接下来需要将每个 span 的信息存储起来.

我们用一个 bitmap 来表示 span 对应原始数组的区间: bitmap 中的一个 bit 代表 16 个数组元素, 置位的位置表示一个 span 的最后一个16个数字的位置, 例如:

001011110000......
<-- least significant bit

在上面这个 bitmap 中的前3个 span 对应的区间分别是:

span[0] 对应nums[0: 48]
span[1] 对应nums[48: 80]
span[2] 对应nums[80: 96]

当需要从数组下标i找到对应的 span 时, 就统计一下 bitmap 中第 i/16 个 bit 之前1的个数:

这个操作非常快, 在go代码中对应的是math/bit.OnesCount()函数(其他语言中也叫做population count), 一般只需要一个汇编指令:

spanIndex = OnesCount(bitmap & (1<<(i/16) - 1))

读取过程

读取过程通过找span, 读取span配置,还原原始数据几个步骤完成, 假设 slimarray 的对象是sa:

  • 通过下标i 得到 spanIndex: spanIndex = OnesCount(sa.bitmap & (1<<(i/16) - 1));
  • 通过 spanIndex 得到多项式的3个系数: [b₀, b₁, b₂] = sa.polynomials[spanIndex: spanIndex + 3];
  • 读取 delta 数组起始位置, 和 delta 数组中每个 delta 的 bit 宽度: config=sa.configs[spanIndex];
  • delta 的值保存在 delta 数组的config.offset + i*config.width的位置, 从这个位置读取width个 bit 得到 delta 的值.
  • 计算 nums[i] 的值: b₀ + b₁*i + b₂*i² 再加上 delta 的值.

简化的读取逻辑如下:

func (sm *SlimArray) Get(i int32) uint32 {

    x := float64(i)

    bm := sm.spansBitmap & bitmap.Mask[i>>4]
    spanIdx := bits.OnesCount64(bm)

    j := spanIdx * polyCoefCnt
    p := sm.Polynomials
    v := int64(p[j] + p[j+1]*x + p[j+2]*x*x)

    config := sm.Configs[spanIdx]
    deltaWidth := config & 0xff
    offset := config >> 8

    bitIdx := offset + int64(i)*deltaWidth

    d := sm.Deltas[bitIdx>>6]
    d = d >> uint(bitIdx&63)

    return uint32(v + int64(d&bitmap.Mask[deltaWidth]))
}

实际实现中, 还将整个数组划分成多个1024元素大小的段, 以减少x变大时产生的误差.

在用曲线拟合的方式中还有一些额外的好处, 例如某些对整个数组的统计操作可以通过曲线的计算来简化:

求和的优化设计

对 slimarray 中一段数据的求和运算会变得非常高效, 对n个数字yᵢ的求和可以转化为简单的数值计算:

\[\begin{aligned} \sum y_i = & \sum\beta_0 + \sumβ_1 i + \sum \beta_2 i^2 + \sum d_i \\ = & \beta_0 n \\ & + \beta_1 \frac{1}{2} n (n+1) \\ & + \beta_2 \frac{1}{6} n (n+1) (2n+1) \\ & + \sum d_i \end{aligned}\]

  • 如果只需要近似结果(忽略Σdᵢ), 那么一个 O(n) 的遍历累加就直接被转换成O(1)的计算.

  • 如果要精确值, 因为dᵢ的宽度比较小, 在实现时将 4 bit 或 8 bit 打包到一个或多个uint64里, 计算求和可以通过 SIMD 指令来优化, 例如对128个 4 bit 数的求和运算就可以通过: _mm512_reduce_add_epi64(_mm512_sad_epu8(a, _mm512_setzero_si512())) 来完成.

如果有必要, 也可以也存储一个span的Σdᵢ的值, 这样每个 span 需要额外的 64bit, 换来的是对 span 范围内的求和操作优化到 O(1) 的复杂度.

slimarray at github

Archive