xp的分布式系统系列教程之: Erasure-Code: 工作原理, 数学解释, 实践和分析.
- 内容简介
- 分布式系统的可靠性问题: 冗余和多副本
- EC的基本原理
- EC编码矩阵的几何解释
- EC解码过程: 求解n元一次方程组
- 新世界: 伽罗华域 [Galois-Field] GF(7)
- EC使用的新世界 [Galois-Field] GF(256)
- 实现
- 分析
- 参考
内容简介
Erasure-Code, 简称 EC, 也叫做 擦除码 或 纠删码, 指使用 范德蒙(Vandermonde) 矩阵的 里德-所罗门码(Reed-Solomon) 擦除码算法.
EC 本身是1组数据冗余和恢复的算法的统称.
本文以 Vandermonde 矩阵的 Reed-Solomon 来解释 EC 的原理.
术语定义:
- $d_j$ 表示数据块.
- $y_i$ 表示通过数据块计算得来的, 作为数据冗余的校验块.
- $u_j$ 表示丢失的, 需要恢复的数据块.
- k 表示数据块的数量.
- m 表示校验块的数量.
本文内容包括:
-
第1节 分布式系统的可靠性问题: 冗余和多副本 提出EC需要解决的问题.
-
希望对分布式存储领域增加了解的同学, 可以只阅读 EC的基本原理 部分.
这部分会用到1些中学的数学知识, 逐步用举栗子🌰的方式给出了EC算法的直观解释.
它和真正实现层面的EC原理是一致的, 但不深入到太多数学层面的内容.
-
已经对EC工作方式有些了解, 希望更深入了解其数学原理的读者, 可以直接从 EC编码矩阵的几何解释 开始阅读.
这部分解释了EC的编码矩阵的原理和含义, 但不包括更底层数学的讨论.
伽罗华域GF(7) 和 伽罗华域GF(256) 开始介绍如何将EC应用到计算机上的方法, 从这部分开始EC会用到1些抽象代数中的知识.
-
需要动手扣腚解决分布式存储问题的猿, 如果对数学原理不感兴趣, 但对工程实践方面有兴趣的话, 可以参考 实现.
-
需要对存储策略规划的架构师, 可以直接参考数值分析部分 分析.
分布式系统的可靠性问题: 冗余和多副本
在分布式系统中, 第1个要解决的问题是可靠性问题, 因为服务器会宕机,磁盘会掉,光纤会被挖掘机铲断, 机房会被大雨淹没. 数据存储多份才可以达到工业可用的可靠性.
一般还必须让数据的多个副本分布在不同的服务器, 机架或机房里才能真正达到高可靠.
数据可靠了之后才需要讨论数据的一致性和性能等问题. (也可能, 一致性和可靠性是并列第一的😄).
提高可靠性也很直接, 一般的解决方式就是 对一份数据存储多个副本.
副本数一般选择3:
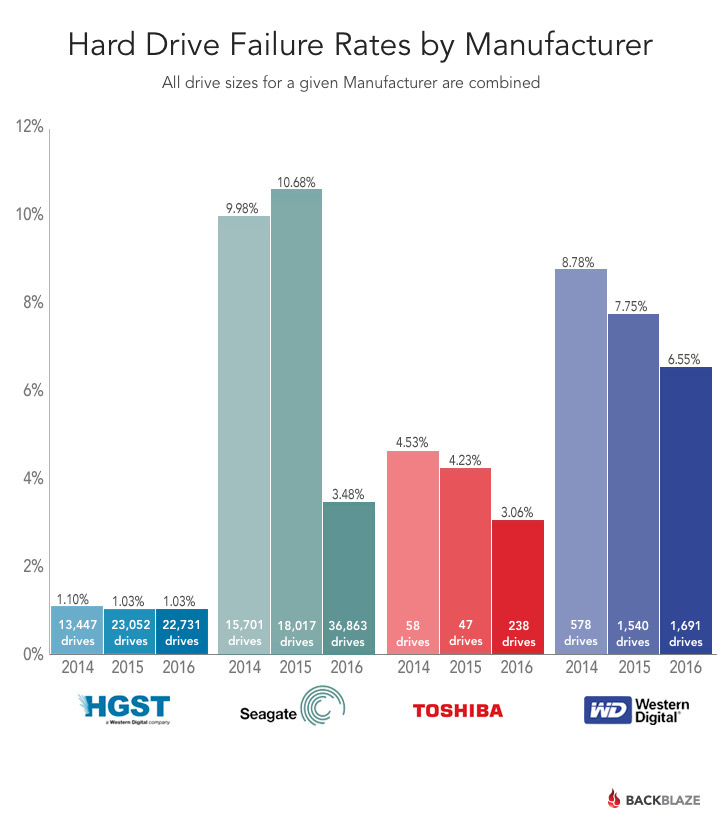
3副本结合当前经验上的磁盘的损坏率(大约是年损坏率7%), 大约可以达到一个工业可接受的可靠性, 这个可靠性的预期大约是11个9以上(99.999999999%的概率不丢数据).
下图摘自 backblaze发布的硬盘故障率统计
如果我有2块数据(每块可能是1个1G大小的电影): $ d_1 $ 和 $ d_2 $, 为了达到高可靠性, 我需要对每个数据复制3份, 并放在不同的服务器上以保证足够分散, 数据在服务器上的保存的位置大概是酱:
\[(d_1, d_1, d_1), \\ (d_2, d_2, d_2), \\ ...\]第1列的$d_1, d_2$在第1个服务器上,
第2列的$d_1, d_2$在第2个服务器上,
第3列的$d_1, d_2$在第3个服务器上.
这种3副本的策略下, 总的存储冗余度是 300%
空间浪费是200%
当然有些时候为了降低成本, 只存储2个副本, 这时冗余度是200%, 也浪费了1倍的空间:
\[(d_1, d_1), \\ (d_2, d_2), \\ ...\]那么, 能否用较少的冗余, 来实现同样较高的可靠性, 就成了分布式存储的一个重要研发的方向.
这就是本文介绍的 EC 需要解决的问题. 接下来, 我们通过几个例子, 1步步介绍 EC 的原理和实现机制.
EC的基本原理
栗子🌰1: 实现k+1的冗余策略, 大概需要小学3年级的数学知识
Q: 有3个自然数, 能否做到再记录第4个数字, 让任何一个数字丢失的时候都可以将其找回?
这个问题很简单, 记录这3个数字的和: 假设3个数字是: $ d_1, d_2, d_3 $; 再存储一个数: $ y_1 = d_1 + d_2 + d_3 $.
-
存储的过程就是存储这4个数字: $ d_1, d_2, d_3, y_1 $:
-
数据丢失后要找回时:
-
这样如果 $ d_1, d_2, d_3 $ 任意一个丢失, 例如 $ d_1 $ 丢失了, 我们都可以通过 $ d_1 = y_1 - d_2 - d_3 $ 来得到 $ d_1 $.
-
如果 $ y_1 $ 丢失, 则再次取 $ d_1 + d_2 + d_3 $ 的和就可以将 $ y_1 $ 找回.
-
在上面这个简单的系统中, 总共存储了4份数据, 有效的数据是3份.
冗余是133%,
它的可靠性和2副本的存储策略差不多: 最多允许丢失1份数据.
看起来这是一个不错的解决方案:
我们用133%的冗余,
实现了和2副本的 200% 冗余 差不多的可靠性! 如下:
| 策略 | 冗余度 | 可靠性 | 存储策略示意 |
|---|---|---|---|
| 2副本 | 200% | 允许丢1块: $ 1 \times 10^{-8} $ | $ (d_1,d_1) $, $ (d_2,d_2)$, $(d_3,d_3)… $ |
| 3+1求和冗余 | 133% | 允许丢1块: $ 6 \times 10^{-8} $ | $ (d_1, d_2, d_3, y_1) $, $ (d_4, d_5, d_6, y_2)… $ |
这里只是差不多, 还并不是完全一样, 后面分析 1节会详细讨论可靠性的计算.
在讨论可靠性的时候, 一般数据丢失风险没有量级的差异, 就可以认为是比较接近的.
上面这个例子是和我们平时使用的 RAID-5 基本是一样的. RAID-5 通过对k个(可能是11个左右)数据块求出1份校验和的数据块. 存储这份校验块, 并允许1块(数据或校验)丢失后可以找回.
当然在工程上, RAID-5 的计算和自然数的求和还有些差异. 后面继续撩.
以上的这种求和冗余策略, 就是 EC 的核心思路.
如果你对存储感兴趣但不希望太多深入细节, 到这里差不多已经比较直观地了解 EC 的原理了.
如果你还有浓厚的兴趣继续读下去,好极!
接下来将上面的内容做些扩展, 后面章节会继续深入1点点, 逐步把上面提到的求和冗余 推广成1个生产环境可用的存储策略, 同时也会逐步引入更多的数学来完善这个策略.
栗子🌰2: 实现k+m的冗余策略, 大概需要初中2年级的数学知识
现在我们在k+1的冗余策略基础上, 增加更多的校验块, 来实现任意k+m的冗余策略.
增加1个校验块, 变成k+2
现在让我们把问题再推进1步. 上面我们通过多增加1份的冗余, 实现了和2副本差不多的可靠性(允许丢失1块数据). 那么我们如果要实现和3副本差不多的可靠性呢(允许丢失2块数据)?
Q: 有3块数据: $ d_1, d_2, d_3 $
可否另外再存储2个冗余的校验块(共5块), 让整个系统任意丢失2份数据时都能找回?
在k+1求和的策略里, 我们实际上是给所有的数据块和校验块建立了一个方程 $ d_1 + d_2 + d_3 = y_1 $, 来描述他们整体的关系.
现在, 如果要增加可丢失的数据块数, 简单的把 $ y_1 $ 存2次是不够的, 假设计算了2个校验块:
\[d_1 + d_2 + d_3 = y_1 \\ d_1 + d_2 + d_3 = y_2 \\ (y_1 = y_2)\]-
存储的过程定义为: 存储 $ d_1, d_2, d_3, y_1, y_2 $ 这5个数字.
-
需要恢复数据时: 如果 $ d_1, d_2 $ 都丢失了($ u_1, u_2 $ 表示), 下面这个关于$ u_1, u_2 $的线性方程是有无穷多解的:
\[\begin{cases} u_1 + u_2 + d_3 = y_1 \\ u_1 + u_2 + d_3 = y_2 \end{cases}\]我们没有办法从这个方程组里解出 $ u_1, u_2 $ 的值, 因为这2个方程是一样的, 没有提供更多的信息.
所以我们现在需要做的是, 设计一个计算第2个校验块 $ y_2 $ 的方法:
使得当 $ d_1, d_2 $丢失时方程组有解.
一个简单直接的思路是, 计算$ y_2 $ 时, 给每个数据 $ d_j $ 增加1个不同的系数:
- 计算$y_1$时, 对每个数字乘以1, 1, 1, 1 …
- 计算$y_2$时, 对每个数字乘以1, 2, 4, 8 …
-
存储的过程任然定义为: 存储 $ d_1, d_2, d_3, y_1, y_2 $ 这5个数字.
-
数据恢复的时候, 如果 $ d_1, d_2 $ 丢失, 同样用 $ u_1, u_2 $表示, 我们可以使用剩下的 $ d_3, y_1, y_2 $ 来建里1个关于 $ u_1, u_2 $ 的二元一次方程组:
解出上面这个方程组, 就找回了丢失的 $ u_1, u_2 $.
感谢对我们负责的初中班主任, 把体育课帮我们改成了数学习题课, 让我们还记得这个二元一次方程组好像通过消元, 就能解出 $ u_1, u_2 $ 的值
<( ̄︶ ̄)>
以上这种加系数计算校验块的方式, 就是RAID-6的基本工作方式:
RAID-6为k个数据块之外再多存储2个校验数据, 当整个系统丢失2块数据时, 都可以找回.
为什么计算 $ y_2 $ 的系数是1, 2, 4, 8…?
系数的选择有很多种方法, 1, 2, 4, 8是其中一个. 只要保证最终丢失2个数字构成的方程组有唯一解就可以. 这里选择1, 2, 3, 4…也可以.
到这里, 有理数下k+2的EC的算法大概就出来了, 我们可以实现k+2的冗余策略, 通过166%的冗余, 实现差不多和三副本300%一样的可靠性.
具体的可靠性计算参见下面的: 分析
实现k+m 的冗余
如果要增加更多的冗余,让EC来实现相当于4副本差不多的可靠性: k+3, 我们需要给上面的策略再增加一个校验块 $ y_3 $,
而 $ y_3 $ 的计算我们需要再为所有的 $ d_j $ 选择1组不同的系数, 例如1,3,9,27…来保证后面数据丢失时,得到的1个3元一次方程组是可解的:
\[\begin{cases} \begin{aligned} d_1 + d_2 + d_3 & = y_1 \\ d_1 + 2 d_2 + 4 d_3 & = y_2 \\ d_1 + 3 d_2 + 9 d_3 & = y_2 \end{aligned} \end{cases}\]这样我们通过不断的增加不同的系数, 就可以得到任意的k+m的EC冗余存储策略的实现.
到此为止, 有理数下的EC算法就介绍完整了. 接下来的章节中, 我们会深入1点, 讨论下为什么要选择这样1组系数.
实际上,现实中使用的RAID-5和RAID-6都是 EC 的子集. EC 是更具通用性的算法. 但因为实现的成本(主要是计算的开销), RAID-5 和 RAID-6在单机的可靠性实现中还是占主流地位.
但随着存储量的不断增大, 百PB的存储已经不算是很极端场景了. RAID-6 在单机环境下不算高的数据丢失风险在大数据量的场景中显示的越来越明显. 于是在云存储(大规模存储)领域, 能支持更多的冗余校验块的EC成为了主流.
EC编码矩阵的几何解释
上面大概介绍了如何选择 EC 生成校验块(编码过程)的系数, 我们隐约可以预感到它的系数选择可能有某种内涵, 下面我们来从最初的问题入手, 讨论下为什么会得出这样1组系数选择的方法.
EC 可以这样被理解: 为了恢复几块数据, 我们需要预先通过这几块数据 $ d_j $ 另外计算出几个数值(校验块), 校验块和数据块构成1个整体, 这些校验块具备所有数据块的特征, 可以用于和其他几个数据配合起来找回丢失的数据块.
我们从比较简单的情况开始, 看下2个数据块计算(多个)EC校验块的方法:
k=2, 为2个数据块生成冗余校验块
假设 现在我们有2个数据块 $ d_1, d_2 $. 要做2个校验块.
我们使用1个直线的方程, 来实现数据的冗余备份和恢复:
$ y = d_1 + d_2 x $
这条直线具备这样的特点:
-
这条直线包含的所有数据块 $ d_j $ 的信息.
任何1对 $ d_1, d_2 $ 的值就确定一条不同的直线. 同样, 任意1条直线也唯一对应1对 $ d_1, d_2 $ 的值.
数据可靠性的问题就转化成了:
- 我们要保存足够多的关于这条直线的信息, 能够在需要的时候找回这条直线. 然后再提取直线方程的系数来找回最初存储的数据块 $ d_1, d_2 $.
要保存足够多的信息, 最直观的方法就是记录这条直线上的几个点的坐标.
因为2点可以确定一条直线, 只要拿到直线上2个点的坐标, 就能确定直线方程, 从而确定它的系数 $ d_1, d_2 $.
按照这样的思路, 我们重新用直线方程的方式描述数据冗余生成和数据恢复的过程:
-
生成冗余的校验数据的过程就是:
在直线上取2个点, 记录点的坐标(这里我们总是取x = [1, 2, 3…]的自然数的值, 所以只记录y的值就可以了)
$ d_1, d_2, (1, y_1), (2, y_2) $
-
恢复数据的过程就是: 已知过直线2点 $ (1, y_1), (2, y_2) $ 来确定直线方程的过程.
再次感谢初中班主任
取 x 分别为 1和2:
\[\begin{cases} y_1 = d_1 + d_2 \\ y_2 = d_1 + 2d_2 \end{cases}\]我们得到了1组带冗余的数据: $ d_1, d_2, y_1, y_2 $. 这4个数据中,任意丢失2个,都可以通过等式关系 $ y = d_1 + d_2 · x $ 来恢复.
丢失1个数据块时只用 $ y_1 $ 的方程就够了.
丢失2个数据块时才需要解二元一次方程组.
如果 $ y_1 $或 $ y_2 $丢失, 则通过重新取点的方式恢复.
我们可以在直线上取任意多个点, 但恢复时最多也只需要2个点就够了. 在这个例子中我们实现了 2+m 的冗余策略.
k=3, 4, 5…时的数据块的冗余
现在我们把它再推广到更一般的情况: 直线方程只需要2个值来确定, 但如果要用描点方式来为更多的数据块生成冗余数据, 我们需要使用高次的曲线, 来记录更多的数据.
例如:
- 二次曲线抛物线 $ y = a x^2 + b x + c $ 需要3个值来确定, 同时也需要知道抛物线上的3个点的坐标来找回这条抛物线.
通过高次曲线生成冗余数据
如果有k个数据块, 我们把k个数据作为系数, 来定义1条关于x的高次曲线:
\[y = d_1 + d_2 x + d_3 x^2 + ... + d_k x^{k-1}\]-
生成m个冗余数据的过程就是:
取m个不同的x的值(1, 2, 3…m), 记录这条曲线上m个不同点的坐标:
$ (1, y_1), (2, y_2) … (m, y_m) $
存储所有的数据块 $ d_1, d_2…d_k $ 和所有的校验块 $ y_1, y_2…y_m $.
-
恢复数据:
当数据丢失时, 我们知道, 平面直角坐标系上m个点可以唯一确定1条 m-1 次幂的关于x的曲线. 确定了这条关于x的曲线,就找回了它的系数,也就是数据块 $ d_1, d_2 … d_k $
以上就是 EC 的算法的几何解释: 通过曲线上的点来确定曲线的过程.
从曲线方程得到的系数矩阵
在曲线方程上取点的坐标的过程中, 我们直接为x取自然数的位置来计算 y 的值: 1, 2, 3…:
\[y_1 = d_1 + d_2 · 1 + d_3 · 1^2 + .. + d_k · 1^{k-1} \\ y_2 = d_1 + d_2 · 2 + d_3 · 2^2 + .. + d_k · 2^{k-1} \\ y_3 = d_1 + d_2 · 3 + d_3 · 3^2 + .. + d_k · 3^{k-1} \\ ... \\\]把上面等式写成矩阵的形式, 得到EC校验块的 生成矩阵 Generator-Matrix:
\[\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ ... \\ y_m \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1^2 & ... & 1^{k-1} \\ 1 & 2 & 2^2 & ... & 2^{k-1} \\ 1 & 3 & 3^2 & ... & 3^{k-1} \\ ... & ... & ... & ... & ... \\ 1 & m & m^2 & ... & m^{k-1} \end{bmatrix} \times \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ ... \\ d_k \end{bmatrix}\]这里 $ y_1, y_2 … y_m $ 就是校验块的数据, 矩阵里就是我们上面使用的这样那组系数.
这个矩阵就是著名的 Vandermonde 矩阵.
Vandermonde 矩阵只是 EC 其中1种系数的选择方式. 其他常用的系数矩阵还有 Cauchy 矩阵等.
EC解码过程: 求解n元一次方程组
现在我们知道, EC 就是:
有1组数字: $ d_1, d_2, d_3…d_k $ 另外记录m个校验用的数字 $ y_1, y_2, y_3…y_m $ 使得这k+m个数字中任意丢失m个都能从剩下的k个中恢复所有的k+m个数字.
EC生成校验块的过程称之为EC的编码, 当数据丢失需要找回的时候, 使用的是EC的解码过程.
如上面章节所说, EC的编码过程是编码矩阵(Vandermonde)和数据块列相乘:
\[\begin{bmatrix} 1 & 1 & 1 & ... & 1 \\ 1 & 2 & 4 & ... & 2^{k-1} \\ 1 & 3 & 9 & ... & 3^{k-1} \\ ... \\ 1 & m & m^1 & ... & m^{k-1} \end{bmatrix} \times \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ ... \\ d_k \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ ... \\ y_m \end{bmatrix}\]解码的过程如下:
假设有q个数字丢失了, $ q \le m $. 从上面的编码矩阵中选择 $ y_1, y_2..y_q $, q行, 组成的一次方程组, 求解丢失的数据.
例如 $ d_2, d_3 $ 丢失了, 下面用 $ u_2, u_3 $ 表示 (只丢失了2块数据, 不需要所有的m个校验块参与, 只需要2个校验块来恢复数据)
\[\begin{bmatrix} 1 & 2 & 4 & ... & 2^{k-1} \\ 1 & 3 & 9 & ... & 3^{k-1} \\ \end{bmatrix} \times \begin{bmatrix} d_1 \\ u_2 \\ u_3 \\ ... \\ d_k \end{bmatrix} = \begin{bmatrix} y_2 \\ y_3 \\ \end{bmatrix}\]这个矩阵表示的方程组里有2个未知数 $ u_2, u_3 $, 解方程即可得到 $ u_2, u_3 $ 这2块丢失的数据.
Vandermonde 矩阵保证方程组有解
对于k+m的EC来说, 任意丢失m个数据块都可以将其找回.
Vandermonde 矩阵保证了任意m行m列组成的子矩阵都是线性无关的,
构成的方程肯定有确定解.
Vandermonde 的 行列式的值为:
\[\det(V)=\prod_{1 \leq i \lt j \leq n}(\alpha_j - \alpha_i)\]只要 $ \alpha_i $ 都不同, 则 Vandermonde 矩阵的行列式就不为0, 矩阵可逆, 表示方程有唯一解.
容易证明, Vandermonde 矩阵的任意 $ m \times m $的子矩阵也可以保证永远有唯一解.
到此为止我们讨论了EC在有理数范围内的全部内容. 它是完整的, 但还不能直接应用到计算机的代码开发商.
接下来我们要展开在纯数学和计算机算法之间的问题, 以及我们将通过什么样的手段来解决这些问题, 将EC真正应用到生产环境中.
新世界: 伽罗华域 Galois-Field GF(7)
在实际使用中, 并不像上面的有理数计算那么简单: 就像所有算法在实现中多会面临的问题一样, 在计算机上实现, 必须考虑空间问题. 计算机里不能天然的表示任意自然数, 上面的校验块 $ y_i $ 在计算过程中必然会出现越界问题.
\[y = d_1 + d_2 x + d_3 x^2 + ... + d_k x^{k-1}\]如果我们的数据块 $ d_j $ 的取值范围是1个字节大小,
那么计算出来的校验数据 $ y_i $ 随着x的值的选取, 很可能就超出了1个字节大小,
如果仍然使用这种方式生成校验块, 最终冗余的数据的大小就会变得不可控,
实际存储的冗余会大于 k+m : k 的冗余度, 无法达到有效控制冗余数据大小的目的.
因此上面介绍的EC, 在计算机上实现时, 必须解决数字大小的问题. 但总的算法是不变的. 这次我们要从最底层开始入手, 解决这个问题.
这里所说的最底层, 是指曲线, 多元一次方程等依赖的底层的四则运算法则. 我们将找到另外一套四则运算, 既能满足 EC 计算的需要, 又能很好第控制数值的范围. 我们要将 EC 移植到另一套代数结构上.
这也是我自己在学习 EC 时觉得最有趣的地方:
类似于把一段c代码写好后可以编译到intel CPU上也可以编译到ARM CPU上运行(即使这2种CPU的指令完全不同, 但c源代码的正确性是不变的),
现在我们要做的是, 我们设计好 EC 的上层算法后, 把它移植到另1套代数体系中, 而同时也能保证它上层的”源代码” 在另1种不同的底层体系上也可以正确运行!
EC在计算机里的实现: 基于 伽罗华域 Galois-Field
上面我们提到的几个数学公式, 高次曲线, 多元一次方程组等: $ y = d_1 + d_2 x + d_3 x^2 + … + d_k x^{k-1} $
他们之所以能正确的工作, 是因为他们依赖于一套底层的基础运算规则, 这就是四则运算: $ + - \times \div $ (实现 EC 的代数中我们没有用到开方运算).
这听起来有点废话, ™不用四则运算用什么?
其实我们平时熟知的四则运算, 在代数里并不是唯一的四则运算法则, 它有很多很多个兄弟, 他们有共同的规律,却有着不同的表现形式.
例如在有1种四则运算建立的代数可能是: $ 5 + 5 = 3 $ 而不是10, $ 5 \times 3 = 1 $ 而不是15. 也可能有1种四则运算里乘法不是加法的叠加.
最常见的是钟表的时间相加, 20点加8个小时不是28点, 而是4点.
我们现在需要做的是, 找到一种四则运算, 来让 EC 的计算可以不会越界!
现在我们来一步步开启这扇新世界的大门…
首先感谢19世纪因为跟情敌决斗被一枪打死的伟大数学家 伽罗华.
栗子🌰3: 只有7个数字的新世界: GF(7)
大门, 慢慢开启…
我们来尝试定义一个新的加法规则, 在这个新的世界里只有0~6这7个数字:
其他整数进来时都要被模7, 变成0~6的数字.
在这个模7的新世界里, 四则运算也可以工作:
模7新世界中的 加法
我们来尝试定义一个新的加法规则, 在这个只有0~6这7个数字的新世界里,
(新的加法被表示为 ⊕ (这里原始的加法还是用+来表示)):
它定义为: a ⊕ b的结果是 a + b后结果再对7取模. 例如:
1 ⊕ 1 = 2
5 ⊕ 2 = 0 ( 7 % 7 = 0 )
5 ⊕ 5 = 3 ( 10 % 7 = 3 )
在这个新世界里, 0 还是和以前的0很相像, 任何数跟0相加都不变:
0 ⊕ 3 = 3
2 ⊕ 0 = 2
0 在新世界 GF(7) 里被称为加法的单位元.
模7新世界中的 减法
然后我们再在模7的世界里定义减法. 减法的定义也很直接, 就是加法的逆运算了.
就像自然数里1样, -2 + 2 = 0, 我们称呼-2是2在加法上的逆元(通常称为相反数).
在模7的世界里,我们也很容易找到每个数的加法逆元,例如:
$ 3 ⊕ 4 = 0 $
所以 4 和 3 就互为加法的逆元, 或者说是(新世界的)相反数.
减法定义就是: $ a ⊖ b \rightarrow a ⊕ (-b) $.
例如:
3 ⊖ 4 = 6 ( (-1) % 7 = 6 )
2 ⊖ 6 = 3 ( (-4) % 7 = 3 )
其实我们不需要减法, 我们只需要 加法 和 逆元 的定义
模7新世界中的 乘法 和 除法
在模7的新世界里, 我们也可以类似地定义1个乘法:
\[\begin{equation} a ⊗ b \rightarrow (a \times b) \mod 7 \end{equation}\]例如:
1 ⊗ 5 = 5 ( 5 % 7 = 5 )
3 ⊗ 4 = 5 ( 12 % 7 = 5 )
2 ⊗ 5 = 3 ( 10 % 7 = 3 )
0 ⊗ 6 = 0
对于模7新世界的乘法⊗来说, 1 是乘法的单位元, 也就是说1 ⊗ 任何数都是它本身.
我们也可以用类似的方法定义每个数字在乘法⊗的逆元:
a的乘法逆元 $ a^{-1} = b, iff a ⊗ b = 1 $.
例如:
\[\begin{aligned} 3^{-1} & = 5 ( 3 \times 5 \% 7 = 1 ) \\ 4^{-1} & = 2 ( 4 \times 2 \% 7 = 1 ) \end{aligned}\]除法的定义就是: 乘以它的乘法逆元
栗子🌰4: 模7新世界直线方程-1
现在我们有了新的加法和减法⊕, ⊖ 我们可以像使用旧世界的加减法一样来使用⊕, ⊖. 例如我们可以建立一个简单的, 斜率为1的直线方程:
\[y = x ⊕ 3\]新世界里这个直线上的点是: (x,y) ∈ [(0,3), (1,4), (2,5), (3,6), (4,0), (5,1), (6,2)] 只有7个.
如果把这条直线画到坐标系里, 它应该是这个样子的:
y = x ⊕ 3
y
^
6 | •
5 | •
4 | •
3 •
2 | •
1 | •
0 +-------•-----> x
0 1 2 3 4 5 6
栗子🌰5: 模7新世界直线方程-2
再加上新世界加减乘除四则运算, 我们可以在新世界里进行基本的代数运算了, 例如我们可以设定1个斜率为2的直线方程:
\[y = 2 ⊗ x ⊕ 3\]新世界里这个直线上的点是: (x,y) ∈ [(0,3), (1,5), (2,0), (3,2), (4,4), (5,6), (6,1)] 这7个.
如果把这条直线画到坐标系里, 它应该是这个样子的:
y = 2 ⊗ x ⊕ 3
y
^
6 | •
5 | •
4 | •
3 •
2 | •
1 | •
0 +---•---------> x
0 1 2 3 4 5 6
栗子🌰6: 模7新世界中的二次曲线方程
下面我们来建立1个稍微复杂1点的, 二次曲线的方程:
\[y = x^2 ⊕ x ⊕ 2\]这里 $ x^2 $ 表示 $ x ⊗ x $
新世界里这个抛物线上的点集合是: (x,y) ∈ [(0, 2) (1, 4) (2, 1) (3, 0) (4, 1) (5, 4) (6, 2)]
如果把这条抛物线画到坐标系里, 它应该是这个样子的:
y = x^2 ⊕ x ⊕ 2
y
^
6 |
5 |
4 | • •
3 |
2 • •
1 | • •
0 +-----•-------> x
0 1 2 3 4 5 6
可以看出它的图像也遵循了旧世界抛物线的特性: 这条抛物线是以3为轴对称的: 因为类似旧世界的多项式分解一样, 原方程也可以分解成:
\[\begin{aligned} y & = (x ⊕ (-3))^2 \\ & = x^2 ⊕ (-6)x ⊕ 9 \\ & = x^2 ⊕ x ⊕ 2 \end{aligned}\]模7新世界里的EC
在这个模7的新世界里, 它满足我们旧世界里的四则运算法则, 我们已经可以使用上面提到的 EC 的算法来编码或解码了:
假设模7新世界里我们的数据块 $ d_1 = 3, d_2 = 2 $, 对应上面的直线方程: y = 2 ⊗ x ⊕ 3
我们只要记住2个点的位置, 就能把直线的方程恢复出来:
例如:
-
我们先记录直线上2个点: (1,5) 和 (3,2)
-
假设丢失的数据是 $ d_1, d_2 $ 用 $ u_1, u_2 $ 表示, 带入2个点的坐标, 得到一个二元一次方程组:
\[\begin{cases} \begin{aligned} 5 & = u_2 ⊕ u_1 \\ 2 & = u_2 ⊗ 3 ⊕ u_1 \end{aligned} \end{cases}\]2个方程左右分别相减消元:
\[\begin{aligned} 5 ⊕ (-2) & = u_2 ⊗ (1 ⊕ (-3)) ⊕ u_1 ⊕ (-u_1) \\ 5 ⊕ 5 & = u_2 ⊗ (1 ⊕ 4) \\ 3 & = u_2 ⊗ 5 \end{aligned}\]最后得到 $ u_2 = 3 ⊗ 5^{-1} = 3 ⊗ 3 = 2 $.
将$ u_2 = 2 $ 带入第1个方程:
$ 5 = 2 ⊗ 1 ⊕ u_1 $
得到 $ u_1 $:
$ u_1 = 5 ⊕ (-2) = 3 $
至此, 我们用模7新世界的四则运算实现了之前的 EC . 并且我们保证了校验数据的大小是可控的: 不会大于7! 距离我们的目标又接近了1步.
类似的, 我们可以通过模7新世界的抛物线, 来实现k=3, k=4的 EC.
NOTE:
模7下的四则运算构成了1个 伽罗华域 Galois-Field: $ GF(7) $.模7是1个可选的数, 也可以选择模11或其他质数来构造1个 Galois-Field, 但是不能选择模一个合数来建立新的四则运算规则. 假设使用模6, 模6世界里面的2是6的一个因子, 它没有乘法逆元, 也即是说2 乘以 1~5任何一个数在模6的世界里都不是1.
没有乘法逆元就说明模6的世界里没有和旧世界里一样的除法, 不能构成一个完整的四则运算体系.
NOTE:
为了简化本文, 四则里还有几个方面没有提到, 例如乘法加法的分配率. 乘法和加法的结合律也必须满足, 才能在新世界里实现上面例子中的曲线方程等元素. 这部分也很容验证,在上面的模7新世界里是可以满足的.
现在我们有了 EC 的算法, 以及很多个可以选择的四则运算来限定数值的范围. 接下来要在计算机上实现,还有1步,就是: 模7虽然可取,但是它没有办法对计算机里的数字有效利用,因为计算机里的数是二进制的. 如果把数值限定到7或其他质数上,没有办法实现256或65536这样的区间的有效利用.
所以接下来我们需要在所有四则运算里选择一个符合计算机的二进制的四则运算, 作为实现 EC 计算的基础代数结构.
EC使用的新世界 Galois-Field GF(256)
从现在开始, 我们要构造一个现实中真实可以用的伽罗华域, 它比上面模7新世界稍微复杂一点, 得到这个域分为2步:
-
我们首先选择1个基础的, 只包含2个元素的 Galois-Field $ GF(2) $: {0, 1}.
-
再在这个 $ GF(2) $ 的基础上建立1个有256个元素的 Galois-Field $ GF(2^8) $.
模2的新世界: Galois-Field GF(2)
首先我们要构建一个最基础的四则运算, 我们先选择了最小的1个Galois-Field, 里面只有2个元素{0,1}:
在这个GF(2)里, 运算的规则也非常简单:
-
加法(刚好和位运算的
异或等价):0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 01的加法逆元就是1 本身.
-
乘法(刚好和位运算的
与等价):0 ⊗ 0 = 0
0 ⊗ 1 = 0
1 ⊗ 0 = 0
1 ⊗ 1 = 11的乘法逆元就是1 本身. 0 没有乘法逆元.
以这个GF(2)为基础, 我们已经可以构建一个1-bit的 EC 算法了:)
下一步我们希望构建1个1 byte大小($ 2^8 $ 个元素)的 Galois-Field $ GF(2^8) $, 在这个 $ GF(2^8) $ 里的 EC 中, 的每个$ d_j $ 和 $ y_i $的取值范围可以是0~255.
有点类似于把0~9这10个自然数通过增加进位这个概念后 扩展成能表示任意大小的多位的10进制自然数, 我们通过类似的方法把{0,1}这个$ GF(2) $ 扩大, 引入多项式:
我们使用 GF(2) 的元素作为系数, 定义1个多项式:
\[a_n x^n + ... + a_2 x^2 + a_1 x^1 + a_0 \\ a_i \in GF(2) = \{0,1\}\]$ a_i $ 的四则运算还是遵循 GF(2) 的规则的, 而多项式的四则运算,基于它的系数的四则运算建立:
例如多项式的加法:
-
因为 1 + 1 = 0, 所以:
$ (x + 1) + (1) = x $
-
x的同指数幂的系数相加遵循系数的Field的加法规则, 1 + 1 = 0:
$ (x^2 + x + 1) + (x) = x^2 + 1 $
-
2个相同的多项式相加肯定是0:
$ (x^2 + x + 1) + (x^2 + x + 1) = 0 $
多项式的乘法和旧世界的多项式乘法类似, 仍然是通过乘法的分配率展开多项式:
\[\begin{aligned} (x + 1) (x + 1) & = x (x+1) + (x+1) \\ & = x^2 + x + x + 1 \\ & = x^2 + 1 \end{aligned}\]多项式的除法依旧使用旧世界的多项式长除法法则, 唯一不同仍旧是系数的四则运算是基于GF(2)的:
例如:
\[\begin{aligned} \frac{x^3 + 1}{x + 1} = x^2 + x + 1 \end{aligned}\]多项式的除法的取余计算也类似:
\[x^2 + x + 1 = x (x+1) + 1 \\ (x^2 + x + 1) = 1 \pmod (x+1)\]现在我们通过把 GF(2) 应用到多项式的系数上, 得到了1个包含无限多个元素的多项式的集合 (它还不是一个伽罗华域, 因为缺少除法逆元. 就像整数全集也不是一个伽罗华域, 它也缺少除法逆元),
然后我们还发现, 这些多项式和二进制数是有一一对应关系的, 多项式中指数为i的项的系数就是二进制数第i位的值:
\[\begin{aligned} 1 & \rightarrow 1 \\ x^2 + 1 & \rightarrow 101 \\ x^3 + x & \rightarrow 1010 \end{aligned}\]现在我们可以使用多项式表达的二进制整数的全集. 然后就像上面栗子中的 GF(7) 那样, 通过取模的方式, 将多项式的集合构造1个取模的伽罗华域.
类似的, 现在我们需要找到1个质的多项式(Prime-Polynomial), 来替代GF(7)中7的角色, 并应用到GF(2)为系数的多项式的集合中, 最终得到1个有256个元素的多项式的伽罗华域 $ GF(2^8) $.
首先让我们来熟悉下如何从较小的域扩张到较大的域.
域的扩张 Field-Extension
域的扩张大家应该是非常熟悉的, 只是一般并没有用这个专用的称呼去描述我们平时见到的扩展.
域的扩张经常是通过多项式来完成的.
栗子🌰7: 实数到虚数的扩张
例如我们首先有了实数, 以实数为系数的多项式中, 如果我们选择一个多项式来构造一个方程:
\[\begin{equation} x^2 + 1 = 0 \end{equation}\]这个方程在实数域里是无解的, 但在复数范围内是有解的: $ x = \pm \sqrt{-1} = \pm i $.
这样通过一个实数系数的, 但在实数域中没有根的方程, 我们得到了复数 Complex-Number 的定义,
复数就是: 所有实系数多项式模 $ x^2+1 $ 的余多项式的集合:
\[\mathbb {C} =\mathbb {R} [X]/(X^{2}+1).\]上面所有的余多项式可以表示为: $ a x + b $, a, b都是实数.
这里$ a x + b $ 就是我们熟悉的复数: 多项式 x 对应虚数单位i, 1对应实数单位1.
而任意2个多项式的四则运算, 也对应复数的四则运算, 例如, 设: $ p(x) = x^2 + 1 $
| 多项式($\pmod{p(x)}$) | 复数 |
|---|---|
| $ x + (x+1) = 2x+1 $ | $ i + (1+i) = 1+2i $ |
| $ x · x = -1 $ | $ i · i = -1 $ |
| $ (3x+1)·(x-2) = -5x-5 $ | $ (1+3i)·(-2+i) = -5-5i $ |
类似于将实数扩张到复数, 我们也可以将GF(2) 扩张到 $ GF(2^8) $.
从2到256: 扩张 GF(2)
域的扩张就是在现有域为系数的多项式中, 找到1个质的多项式 Prime-Polynomial, 再将所有多项式模它得到的结果的集合就是域的扩张.
例如 $ x^2 + 1 $ 在实数域下就是 质多项式, 它无法分解成2个多项式乘积.
栗子🌰8: GF(2) 下的质多项式
-
1 是1个质多项式.
-
$ x + 1 $ 是1个质多项式. 因为它最高次幂是1, 肯定不能再拆分成2个多项式乘积了(只能拆分成1次多项式和常数的乘积).
-
2次的质多项式是: $ P_2(x) = x^2 + x + 1 $. 它在GF(2)的域中不能被拆分成2个1次多项式的乘积.
我们可以像使用7对所有整数取模那样, 用它对所有多项式取模, 模它而产生的所有 余多项式, 包含所有最高次幂小于2的4个多项式: $ 0, 1, x, (x + 1) $
这4个多项式就是 GF(2) 在多项式 $P_2(x)$ 的扩张: 我们把{0, 1} 2个元素的域扩张成 4个元素的域.
这4个多项式可以表示成4个2bit的二进制数:00,01,10,11
GF(2) 扩张成 GF(2^8)
为了扩张到 $ GF(2^8) $ 我们选择的8次幂的质多项式是:
\[P_8(x) = x^8 + x^4 + x^3 + x^2 + 1\]这个8次幂的质多项式,模它的所有余多项式,是所有最高次幂不超过7的多项式, 共256个, 它就是 GF(2) 到 GF(256) 的扩张, 扩张后的元素对应0~255这256个二进制数.
因为多项式和二进制数的直接对应关系, $ P_8(x) $ 对应:
- 二进制: 1 0001 1101
- 16进制: 0x11d
而GF(256)中的四则运算如下:
-
加法: $ a ⊕ b $ 对应多项式加法, 同时它表示的二进制数的加法对应: a ^ b
-
乘法: $ a ⊗ b $ 对应多项式的乘法(模$P_8(x)$):
总结一下GF(256)能够满足EC运算的几个性质:
- 加法单位元: 0
- 乘法单位元: 1
- 每个元素对加法都有逆元(可以实现减法): 逆元就是它本身( (x+1) + (x+1) = 0 )
- 每个元素对乘法都有逆元(除了0)(可以实现除法):$P_8(x)$是不可约的, 因此不存在a和b都不是0但ab=0; 又因为GF(256)只有255个非0元素, 因此对a,总能找到1个x使得 $ a^x = a $. 所以 $a^{x-2} a = 1$ $ a^{x-2} $是a的乘法逆元.
- 乘法和加法满足分配率: 基于多项式乘法和加法的定义.
满足这些性质的四则运算, 就可以用来建立高次曲线, 进而在GF(256)上实现EC.
实现
标准EC的实现
以上讨论的是标准的EC的原理, 现在我们将以上的内容总结, 应用到实践上面.
-
四则运算基于 $ GF(2^8) $ 或 $ GF(2^{16}), GF(2^{32}) $, 分别对应1字节, 2字节或4字节.
-
$ GF(2^8) $ 下的加减法直接用
异或计算, 不需要其他的工作. -
$ GF(2^8) $ 下的乘法和除法用查表的方式实现.
首先生成 $ GF(2^8) $ 下对2的指数表和对数表, 然后把乘除法转换成取对数和取幂的操作:
以 $ GF(2^8) $ 为例:
-
生成指数表 $ 2^0, 2^1, 2^2… $的表, 表中元素 $ p_i = 2^i $.
-
生成对数表, 表中元素 $ l_i = log_2i $.
生成2个表的代码很简单, 用python表示如下:
power, log = [0] * 256, [0] * 256 n = 1 for i in range(0, 256): power[i] = n log[n] = i n *= 2 # modular by the prime polynomial: P_8(x) = x^8 + x^4 + x^3 + x^2 + 1 if n >= 256: n = n ^ 0x11d log[1] = 0 # log[1] is 255, but it should be 0指数表: 01 02 04 08 10 20 40 80 1d 3a 74 e8 cd 87 13 26 4c 98 2d 5a b4 75 ea c9 8f 03 06 0c 18 30 60 c0 9d 27 4e 9c 25 4a 94 35 6a d4 b5 77 ee c1 9f 23 46 8c 05 0a 14 28 50 a0 5d ba 69 d2 b9 6f de a1 5f be 61 c2 99 2f 5e bc 65 ca 89 0f 1e 3c 78 f0 fd e7 d3 bb 6b d6 b1 7f fe e1 df a3 5b b6 71 e2 d9 af 43 86 11 22 44 88 0d 1a 34 68 d0 bd 67 ce 81 1f 3e 7c f8 ed c7 93 3b 76 ec c5 97 33 66 cc 85 17 2e 5c b8 6d da a9 4f 9e 21 42 84 15 2a 54 a8 4d 9a 29 52 a4 55 aa 49 92 39 72 e4 d5 b7 73 e6 d1 bf 63 c6 91 3f 7e fc e5 d7 b3 7b f6 f1 ff e3 db ab 4b 96 31 62 c4 95 37 6e dc a5 57 ae 41 82 19 32 64 c8 8d 07 0e 1c 38 70 e0 dd a7 53 a6 51 a2 59 b2 79 f2 f9 ef c3 9b 2b 56 ac 45 8a 09 12 24 48 90 3d 7a f4 f5 f7 f3 fb eb cb 8b 0b 16 2c 58 b0 7d fa e9 cf 83 1b 36 6c d8 ad 47 8e 01对数表(0没有以2为底的对数): 00 00 01 19 02 32 1a c6 03 df 33 ee 1b 68 c7 4b 04 64 e0 0e 34 8d ef 81 1c c1 69 f8 c8 08 4c 71 05 8a 65 2f e1 24 0f 21 35 93 8e da f0 12 82 45 1d b5 c2 7d 6a 27 f9 b9 c9 9a 09 78 4d e4 72 a6 06 bf 8b 62 66 dd 30 fd e2 98 25 b3 10 91 22 88 36 d0 94 ce 8f 96 db bd f1 d2 13 5c 83 38 46 40 1e 42 b6 a3 c3 48 7e 6e 6b 3a 28 54 fa 85 ba 3d ca 5e 9b 9f 0a 15 79 2b 4e d4 e5 ac 73 f3 a7 57 07 70 c0 f7 8c 80 63 0d 67 4a de ed 31 c5 fe 18 e3 a5 99 77 26 b8 b4 7c 11 44 92 d9 23 20 89 2e 37 3f d1 5b 95 bc cf cd 90 87 97 b2 dc fc be 61 f2 56 d3 ab 14 2a 5d 9e 84 3c 39 53 47 6d 41 a2 1f 2d 43 d8 b7 7b a4 76 c4 17 49 ec 7f 0c 6f f6 6c a1 3b 52 29 9d 55 aa fb 60 86 b1 bb cc 3e 5a cb 59 5f b0 9c a9 a0 51 0b f5 16 eb 7a 75 2c d7 4f ae d5 e9 e6 e7 ad e8 74 d6 f4 ea a8 50 58 af在计算 $ GF(2^8) $中的乘法 将 a, b 通过查对数表和指数表实现: $ a \times b = 2^{log_2a+log_2b} $.
NOTE:
Galois-Field 的计算目前实现都是基于查表的, 所以选择大的域虽然可以一次计算多个字节, 但内存中随机访问一个大表也可能会造成cache miss太多而影响性能.一般CPU都没有支持GF乘除法的指令, 但有些专用的硬件卡专门加速GF的乘除法.
-
-
生成GF后, 选择一个系数矩阵, 常用的是 Vandermonde 或 Cauchy.
EC编码: 校验数据生成
通常使用1个矩阵来表示输入和输出的关系 (而不是像上文中只使用校验块的生成矩阵), 这里选择自然数生成的 Vandermonde 矩阵:
\[\begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 1 \\ \hline \\ 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 2^2 & \dots & 2^{k-1} \\ 1 & 3 & 3^2 & \dots & 3^{k-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & m & m^2 & \dots & m^{k-1} \end{bmatrix} \times \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ ... \\ d_k \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ ... \\ d_k \\ y_1 \\ y_2 \\ y_3 \\ ... \\ y_m \end{bmatrix}\]这个矩阵里上面是1个大小为k的单位矩阵, 表示 $ d_j $ 的输入和输出不变.
下面一部分是1个 $ m \times k $ 的矩阵表示校验块的计算.
对要存储的k组数据, 逐字节读入, 形成 $ d_1, d_2…d_k $, 进行矩阵乘法运算, 得到最后要存储的 k 个数据块和 m 个校验块.
之所以把单位矩阵也放到编码矩阵上面, 看起来没有什么用, 只是把输入无变化的输出出来的这种风格, 原因在于在编码理论中, 并不是所有的生成的Code都是k个原始数据 和 m个校验数据的形式, 有些编码算法是将k个输入变成完全不1样的
\[\begin{pmatrix} 1&1&0&1\\ 1&0&1&1\\ 1&0&0&0\\ 0&1&1&1\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{pmatrix}\]k+m个输出, 对这类编码算法, 需要1个k*(k+m)的编码矩阵来表示全部的转换过程. 例如著名的 Hamming-7-4 编码的编码矩阵(输入k=4, 输出k+m=7):EC中也使用了
k*(k+m)的编码矩阵.
EC解码
当数据损坏时, 通过生成解码矩阵来恢复数据:
对所有丢失的数据,
将它对应的第i行从编码矩阵中移除,
移除后, 保留编码矩阵的前k行,
构成1个k*k的矩阵.
例如第 2, 3个数据块丢失, 移除第2, 3行, 保留第k+1和k+2行: 这时矩阵, 数据块(没丢失的和丢失的), 没丢失的数据块($ d_1, d_4, d_5… $), 校验块($ y_1, y_2 $)的关系是:
\[\begin{bmatrix} 1 & 0 & 0 & 0 & \dots & 0 \\ 0 & 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \dots & 1 \\ 1 & 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 2^2 & 2^3 & \dots & 2^{k-1} \\ \end{bmatrix} \times \begin{bmatrix} d_1 \\ u_2 \\ u_3 \\ d_4 \\ ... \\ d_k \end{bmatrix} = \begin{bmatrix} d_1 \\ d_4 \\ ... \\ d_k \\ y_1 \\ y_2 \\ \end{bmatrix}\]最后求逆矩阵, 和没有丢失的块相乘, 就可以恢复出丢失的数据块 $ u_2, u_3 $:
\[\begin{bmatrix} d_1 \\ u_2 \\ u_3 \\ d_4 \\ ... \\ d_k \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & \dots & 0 \\ 0 & 0 & 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \dots & 1 \\ 1 & 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 2^2 & 2^3 & \dots & 2^{k-1} \\ \end{bmatrix}^{-1} \times \begin{bmatrix} d_1 \\ d_4 \\ ... \\ d_k \\ y_1 \\ y_2 \\ \end{bmatrix}\]因为只有 $ u_2, u_3 $ 丢失了, 矩阵相乘时只需要计算逆矩阵的第2, 3行.
Vandermonde 矩阵的可逆性
实数下的Vandermonde 矩阵是一定可逆的, 但它的任意n行n列组成的子矩阵不一定是可逆的.
假设一个 Vandermonde 矩阵, 如果存在一个 $ [ a_1, a_2, a_3 ] $, 使得乘积为全0, 则矩阵n列是线性相关的:
\[\begin{bmatrix} 1 & 1 & 1 \\ 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ \end{bmatrix} \times \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]因为方程: $ a_1 + a_2 x + a_3 x^2 = 0 $ 最多只有2个解, 但原矩阵 要求有3个不同的值 $ 1, x_1, x_2 $ 满足这个方程. 因此不存在这一的 $ a_i $ 使得 Vandermonde 矩阵线性相关.
但如果查看一个 Vandermonde 矩阵的子矩阵($ 0 < u < v $):
\[\begin{bmatrix} 1 & 1 & 1 \\ 1 & x_1^u & x_1^v \\ 1 & x_2^u & x_2^v \\ \end{bmatrix} \times \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]因为方程: $ a_1 + a_2 x^u + a_3 x^v = 0 $ 最多有v个解, 只要v 大于2, 就可能找到一组 $ a_i $ 和 $ x_i $, 使得上面的子矩阵线性相关.
例如, 一个子矩阵, x=-1 时, 矩阵不可逆:
\[\begin{bmatrix} 1 & 1 \\ 1 & x^2 \\ \end{bmatrix}\]GF256 下的 Vandermonde 矩阵的可逆性
在 $ GF(2^8) $ 下的 Vandermonde 矩阵, 除了上面的的不可逆情况外, 还有另外一种情况导致子矩阵不可逆.
举例来说, 以下矩阵是缺失 $ u_1, u_4 $ 情况下的用来恢复数据的矩阵, 它可能不可逆: 如果 $ x^3 == 1 $,
由于2是1个生成元, 容易看出, $ x = 2^{85} $ 是1个不可逆的情况: $ x^3 = 1 $ 于是第1列和第4列完全一样.
\[\begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & x & x^2 & x^3 & x^4 \\ \end{bmatrix}\]Cauchy 矩阵的任意n行n列组成的矩阵都是可逆的, 因为任意子矩阵还是 Cauchy矩阵.
数据恢复IO优化: LRC: [Local-Reconstruction-Code]
当 EC 进行数据恢复的时候, 需要k个块参与数据恢复, 直观上, 每个数据块损坏都需要k倍的IO消耗.
为了缓解这个问题, 一种略微提高冗余度, 但可以大大降低恢复IO的算法被提出: [Local-Reconstruction-Code], 简称 LRC.
LRC的思路很简单, 在原来的 EC 的基础上, 对所有的数据块分组对每组在做1次 $ k’ + 1 $ 的 EC. k’ 是二次分组的每组的数据块的数量.
LRC 的校验块生成
\[\begin{aligned} \overbrace{d_1 + d_2 + d_3}^{y_{1,1}} + \overbrace{d_4 + d_5 + d_6}^{y_{1,2}} & = y_1 \\ d_1 + 2d_2 + 2^2d_3 + 2^3d_4 + 2^4d_5 + 2^5d_6 & = y_2 \\ d_1 + 3d_2 + 3^2d_3 + 3^3d_4 + 3^4d_5 + 3^5d_6 & = y_3 \end{aligned}\]最终保存的块是所有的数据块: $ d_1, d_2, d_3, d_4, d_5, d_6 $, 和校验块 $ y_{1,1}, y_{1,2}, y_2, y_3 $.
这里不需要保存 $ y_1 $ 因为 $ y_1 = y_{1,1} + y_{1,2} $
对于 LRC的EC来说, 它的生成矩阵前k行不变, 去掉了标准EC的第k+1行, 多出2个局部的校验行:
\[\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \hline \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 \\ \hline \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ \end{bmatrix} \times \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \\ y_{1,1} \\ y_{1,2} \\ y_2 \\ y_3 \\ \end{bmatrix}\]LRC 的数据恢复
LRC 的数据恢复和标准的EC类似, 除了2点不同:
-
在选择校验块的行生成解码矩阵的时候, 如果某第k+i行没有覆盖到任何损坏的数据的话, 是无法提供有效性信息, 需要跳过的.
例如 $ d_4 $ 损坏时, 不能像标准EC那样选择第7行
1 1 1 0 0 0这行作为补充的校验行生成解码矩阵, 必须略过第7行, 使用第8行. -
不是所有的情况下, m个数据损坏都可以通过加入m个校验行来恢复. 因为LRC的生成矩阵没有遵循 Vandermonde 矩阵的规则, 不能保证任意k行都是满秩的.
工程优化
插播一条广告: 徐同学的博客中给出了很好的EC工程实现的介绍, 推荐!: 实现高性能纠删码引擎
分析
可靠性分析
在可靠性方面, 假设 EC 的配置是k个数据块, m个校验块. 根据 EC 的定义,k+m个块中, 任意丢失m个都可以将其找回. 这个 EC 组的丢失数据的风险就是丢失m+1个块或更多的风险:
\[\sum_{i=m+1}^{k+m} {k+m \choose i} p^{i} (1-p)^{k+m-i}\]这里p是单块数据丢失的风险,一般选择磁盘的日损坏率: 大约是0.0001.
p一般很小所以近似就只看第1项:
2个校验块和3副本的可靠性对比(取m=2):
| k | m | 丢数据风险 |
|---|---|---|
| 1 | 2 | $ 1 \times 10^{-12} $ (1个数据块+2个校验块 可靠性 和 3副本等价) |
| 2 | 2 | $ 3 \times 10^{-12} $ |
| 3 | 2 | $ 9 \times 10^{-12} $ |
| 10 | 2 | $ 2 \times 10^{-10} $ (10+2 和 12盘服务器的 RAID-6 等价) |
| 32 | 2 | $ 5 \times 10^{-9} $ |
| 64 | 2 | $ 4 \times 10^{-8} $ |
3个校验块和4副本的可靠性对比(取m=3):
| k | m | 丢数据风险 |
|---|---|---|
| 1 | 3 | $ 1 \times 10^{-16} $ (1个数据块+3个校验块 可靠性 和 4副本等价) |
| 2 | 3 | $ 5 \times 10^{-16} $ |
| 3 | 3 | $ 2 \times 10^{-15} $ |
| 10 | 3 | $ 7 \times 10^{-14} $ |
| 32 | 3 | $ 5 \times 10^{-12} $ |
| 64 | 3 | $ 7 \times 10^{-11} $ |
4个校验块和5副本的可靠性对比(取m=4):
| k | m | 丢数据风险 |
|---|---|---|
| 1 | 4 | $ 1 \times 10^{-20} $ (1个数据块+4个校验块 可靠性 和 5副本等价) |
| 2 | 4 | $ 6 \times 10^{-20} $ |
| 3 | 4 | $ 2 \times 10^{-19} $ |
| 10 | 4 | $ 2 \times 10^{-17} $ |
| 32 | 4 | $ 4 \times 10^{-15} $ |
| 64 | 4 | $ 1 \times 10^{-13} $ |
IO消耗
以一个 EC 组来分析, 1个块损坏的概率是 $ p $, 这个组中有块损坏的概率是: $ 1 - (1-p)^{k+m} \approx (k+m)p $
每次数据损坏都需要读取全组的数据进行恢复. 不论1块损坏还是多块损坏, 数据恢复都是读取1次, 输出1或多次. 恢复数据的输出比较小, 1般是1, 所以可以忽略.
每存储一个字节一天数据恢复产生的传输量是(blocksize是一个数据块或校验块的大小):
\[\frac{(k+m)p \times (k+m) \times blocksize} {(k+m) \times blocksize} = (k+m)p\]也就是说, 使用 EC 每存储1TB的数据,
每天(因为我们取的数据损坏概率是按天计算的)用于数据恢复而产生的IO是
k * 0.1GB / TB
磁盘的IO大致上也等同于网络流量, 因为大部分实现必须将数据分布到不同的服务器上.
NOTE:
随着k的增加, 整体成本虽然会下降(1+m/k), 但数据恢复的IO开销也会随着k(近似于)线性的增长.
例如:
假设k+m = 12:
如果整个集群有 100PB 数据,
每天用于恢复数据的网络传输是 100TB.
假设单台存储服务器的容量是30TB,
每台服务器每天用于数据恢复的数据输出量是 30GB,
如果数据恢复能平均到每天的每1秒, 最低的带宽消耗是:
30GB / 86400 sec/day = 3.0Mbps.
但一般来说数据恢复不会在时间上很均匀的分布, 这个带宽消耗需要预估10倍到100倍.
参考
- Vandermonde
- 范德蒙矩阵
- Cauchy
- RAID-5
- RAID-6
- Finite-Field
- Galois-Field
- 伽罗华域
- Reed-Solomon
- 里德-所罗门码
- Erasure-Code
- Prime-Polynomial
- Field-Extension
- Complex-Number
- Hamming-7-4
- Generator-Matrix
Archive
- 15 Nov 2020 slimarray: gzip的压缩率, 即时访问
- 28 Oct 2020 200行代码实现基于paxos的kv存储
- 18 Oct 2020 后分布式时代: 多数派读写的'少数派'实现
- 20 Dec 2019 Art of Pull Requests(翻译)
- 21 Nov 2019 掐指算算: 你的CDN多花了几百万?
- 19 Nov 2019 一年的素描练习
- 30 Oct 2019 互联网中对象访问频率的91分布
- 09 Jan 2019 哄好面试官系列-1: 比较2个python dict(多级)是否相同
- 04 Nov 2018 存储中的文件合并策略优化
- 27 Sep 2018 软件工程是个面包机
- 26 Aug 2018 程序员必须知道的事情, 一般人我不告诉他
- 16 Aug 2018 cgexec 无法继承 LD_PRELOAD 环境变量
- 04 Aug 2018 mysql group replication实践记录: 步骤, 问题和注意事项
- 13 Feb 2018 枚举所有整勾股数
- 03 Feb 2018 ansible中的include, include_tasks 和 import_tasks 的差别
- 20 Nov 2017 python 并发subprocess.Popen的坑
- 05 Aug 2017 程序员必读: 摸清hash表的脾性
- 06 May 2017 python 进程内存增长问题, 解决方法和工具
- 01 Feb 2017 xp的分布式系统系列教程之: Erasure-Code: 工作原理, 数学解释, 实践和分析.
- 01 Feb 2017 xp的分布式系统系列教程之: Erasure-Code: 工作原理, 数学解释, 实践和分析.
- 11 Nov 2015 可靠分布式系统基础 Paxos 的直观解释
- 28 Jul 2015 socket关闭: close()和shutdown()的差异
- 17 May 2015 随手改变世界之 git-auto-squash
- 17 Feb 2015 Numbers Programmers Should Know About Hash
- 11 Feb 2015 Vim-tabbar: Simple, stupid and fast tab-bar for VIM
- 24 Jul 2014 1% 慢请求优化
- 31 Jan 2014 Some useful resources
- 31 Jan 2014 jobq.py -- Queue processing engine