of drdr.xp Blog drdrxp @weibo.com
on math hash

Numbers Programmers Should Know About Hash

There is a hash table:

  • It has b buckets.
  • It has n keys stored in it.
  • We assume that the hash function distributes keys uniformly.
  • A bucket can contain more than 1 keys.

If n \(\approx\) b, the hash table would look like this:

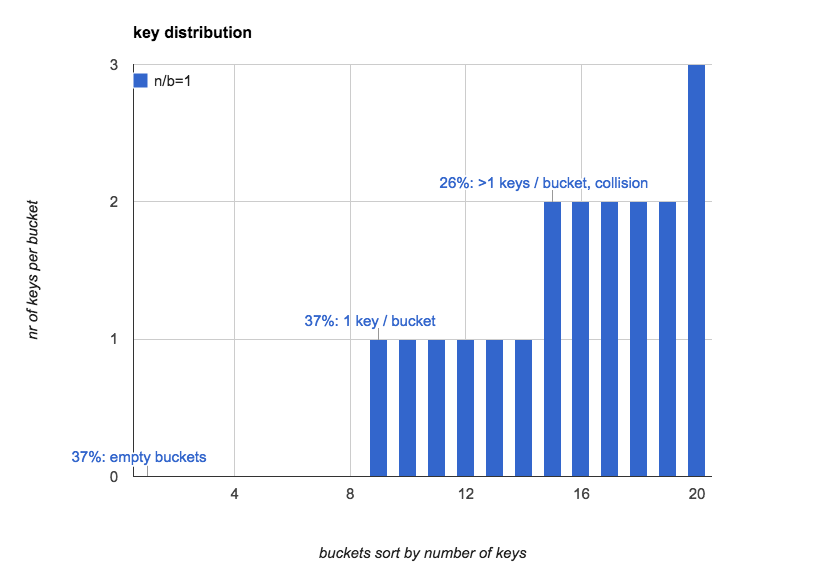
  • 37% buckets are empty.
  • 37% buckets contain 1 key.
  • 26% buckets contain more than 1 key, which means collision occurs.

The following chart created by program simulation shows distribution of 20 keys over 20 buckets.

Load Factor and Key Distribution

Let load factor \(\alpha\) be: \(\alpha = \frac{n}{b}\). load factor defines almost everything in a hash table.

Load Factor <0.75

Normally in-memory hash table implementations keep load factor lower than 0.75. This makes collision rate relatively low, thus looking up is very fast. The lower the collision rate is, the less the time it takes to resolve collision, since linear-probing is normally used and it is very sensitive to collision rate.

In this case, there are about 47% buckets empty. And nearly half of these 47% will be used again by linear-probing.

As we can see from the first chart, when load factor is small, key distribution is very uneven. What we need to know is how load factor affects key distribution.

Increasing load factor would reduce the number of empty buckets and increase the collision rate. It is monotonic but not linear, as the following table and the picture shows:

Load factor, empty buckets, buckets having 1 key and buckets having more than 1 keys:

load factor(n/b) 0 1 >1
0.5 61% 30% 9%
0.75 47% 35% 17%
1.0 37% 37% 26%
2.0 14% 27% 59%
5.0 01% 03% 96%
10.0 00% 00% 100%

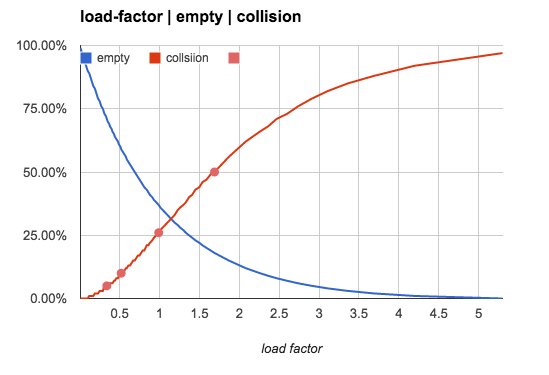
0.75 has been chosen as upper limit of load factor not only because of concerns of collision rate, but also because of the way linear-probing works. But that is ultimately irrelevant.

Tips

  • It is impossible to use hash tables with low space overload and at the same time, with low collision rate.
    • The truth is that just enough buckets waste 37% space.

  • Use hash tables only for (in memory) small data sets.

  • High level languages like Java and Python have builtin hash tables that keep load factor below 0.75.

  • Hash tables do NOT uniformly distribute small sets of keys over all buckets.

Load Factor >1.0

When load factor is greater than 1.0, linear-probing can not work any more, since there are not enough buckets for all keys. chaining keys in a single bucket with linked-list is a practical method to resolve collision.

linked-list works well only when load factor is not very large, since linked-list operation has O(n) time complexity. For very large load factor tree or similar data structure should be considered.

Load Factor >10.0

When load factor becomes very large, the probability that a bucket is empty converges to 0. And the key distribution converges to the average.

The higher load factor is, the more uniformly keys are distributed

Let the average number of keys in each bucket be:

\[{avg} = \frac{n}{b}\]

100% means a bucket contains exactly \({avg}\) keys. The following charts show what distribution is like when load factor is 10, 100 and 1000:

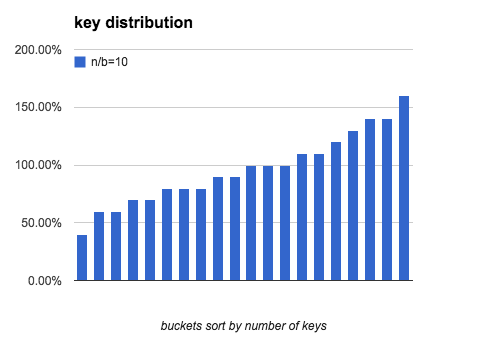
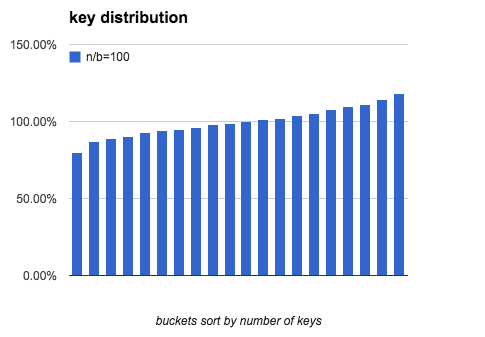
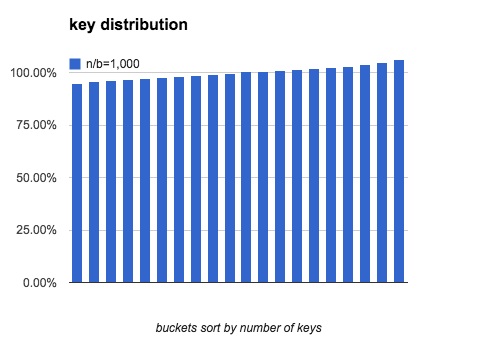
As load factor becomes higher, the gap between the most keys and the fewest keys becomes smaller.

load factor (most-fewest)/most fewest
1 100.0% 0
10 88.0% 2
100 41.2% 74
1,000 15.5% 916
10,000 5.1% 9735
100,000 1.6% 99161

Calculation

Most of the numbers from above are produced by program simulations. From this chapter we are going to see what the distribution is in math.

Expected number of each kind of buckets:

  • 0 key: \(b e^{-\frac{n}{b}}\)
  • 1 key: \(n e^{ - \frac{n}{b} }\)
  • >1 key: \(b - b e^{-\frac{n}{b}} - n e^{ - \frac{n}{b} }\)

Number of Empty Buckets

The chance a certain key is NOT in a certain bucket is: \(\frac{b-1}{b}\). Since: \(\lim_{b\to \infty} (1+\frac{1}{b})^b = e\). The probability of a certain bucket being empty is:

\[(\frac{b-1}{b})^n = ((1- \frac{1}b)^b)^{\frac{n}{b}} = e^{-\frac{n}{b}}\]

Thus the total number of empty buckets is:

\[b e^{-\frac{n}{b}}\]

Number of Buckets Having 1 Key

The probability of a bucket having exactly 1 key is:

\[{n \choose 1} ( \frac{1}{b} )^1 ( 1 - \frac{1}{b} )^{n-1} = \frac{n}{b} e^{-\frac{n}{b}}\]

One of the n keys is in this bucket, and at the same time, no other key is in this bucket:

The the number of buckets having exactly 1 key is:

\[b\frac{n}{b} e^{-\frac{n}{b}} = n e^{ - \frac{n}{b} }\]

Number of Buckets Having More Than One Key

\[b - b e^{-\frac{n}{b}} - n e^{ - \frac{n}{b} }\]

Distribution Uniformity

Similarly, the probability of a bucket having exactly i keys is:

\[p(i) = {n \choose i} ( \frac{1}{b} )^{ i } ( 1 - \frac{1}{b} )^{n-i}\]

The probability distribution is binomial-distribution.

And we want to know how many keys there are in the bucket having the fewest keys and in the bucket having the most keys.

Approximation by Normal Distribution

When n and b are large, binomial-distribution can be approximated by normal-distribution to estimate uniformity.

Let \(p = \frac{1}{b}\). The probability of a bucket having exactly i keys is:

\[p(i) = {n \choose i}p^i(1-p)^{n-i} \approx \frac{1} {\sigma \sqrt{2 \pi} } e^{ - \frac{(i-\mu)^2} {2 \sigma^2} }\]

Where:

\[\mu = np \\ \sigma^2 = np(1-p) \\\]

The probability that a bucket has less than x keys is:

\[P(x) = \sum_{i=0}^x p(i)\]

Thus in this hash table, the total number of buckets having less than x keys is:

\[b \cdot P(x) = b \cdot \sum_{i=0}^x p(i)\]

Choose x so that the total number of such buckets is 1. Then this only bucket must be the one that has the fewest keys. So find x that satisfies:

\[b \cdot \sum_{i=0}^x p(i) = 1\]

With this x, the expected number of keys in this bucket is:

\[N_{min} = \frac{ \sum_{i=0}^x i \cdot p(i) } { \sum_{i=0}^x p(i) } = b \cdot \sum_{i=0}^x i \cdot p(i) \approx b \int_{i=0}^x i \cdot p(i) di\]

Since normal distribution is symmetric:

\[N_{max} + N_{min} = 2 \mu = 2 \frac{n}{b}\]

Find x

Now what we need to do is to find x in order to find \(N_{max}\) and \(\ N_{min}\).

The probability of a bucket that contains less than x keys is:

\[\sum_{i=0}^x p(i) \approx \int_{0}^{x} p(i) di \approx \int_{-\infty}^{x} p(i) di = \Phi( \frac{x-\mu}\sigma )\]

\(\Phi(x)\) is cdf of standard normal distribution. When x - u is close to 0, it is approximated by:

\[\Phi(x)\; =\;0.5+\frac{1}{\sqrt{2\pi}}\cdot e^{-x^2/2}\left[x+\frac{x^3}{3}+\frac{x^5}{3\cdot 5}+\cdots+\frac{x^{2n+1}}{(2n+1)!!} + \cdots\right]\]

By iterating x backward from u to 0, we can find the solution to

\[b \cdot \Phi(\frac{x-\mu}\sigma) = 1\]

Using this x we can find \(N_{min}\) and \(N_{max}\).

Simulations in Python

Several simulation programs used in this post are here: hash-simulation

Reference

Archive