array, 数组, compress, succinct

slimarray: gzip的压缩率, 即时访问

slimarray 是一个静态整数压缩数组, 现实数据达到和gzip相当的压缩率, 无需解压就可以直接使用. slimarray at github

continue reading>>
distributed, replication, paxos, kv, 分布式, 存储

200行代码实现基于paxos的kv存储

用200行代码实现一个基于paxos的kv存储, 以最简洁的形式展示paxos如何运行, 作为 paxos的直观解释 这篇教程中的代码示例部分

continue reading>>
distributed, quorum, majority, replication, paxos, raft, 分布式, 多数派

后分布式时代: 多数派读写的'少数派'实现

paxos可以看做是2次 多数派读写 完成一次强一致读写. 多数派要求半数以上的参与者(paxos中的Acceptor)接受某笔操作. 但 多数派读写 并不一定需要多于半数的参与者, 分布式系统中某些场合的优化, 可以通过减少参与者数量来完成的. 本文介绍这些优化对系统可用性产生的影响, 根据什么标准来选择和调整这些参数.

continue reading>>
pull, request, pr, review, teamwork

Art of Pull Requests(翻译)

原文: Art of Pull Requests

img

正如我之前写的， 我们是一个远程团队，团队成员遍布世界各地。 这意味着code reviews 和 pull requests必须远程完成。

最近，我们团队的一位成员提出了这样的宣言:

作为 PR writer 我会:

  • 保持PR够小
  • 使用标签表明PR是许多部分之一
  • 发布PR后在Slack上也提一下

作为 PR reviewer 我会:

  • 一有空就review。
  • 只要比以前好就批准吧.
  • 尽量不要reject一个PR, 有时可以发一个tiket来作为这个PR的补充, 或要求下一个PR来补充这个PR.
  • 建议而不是拒绝，特别是当用标签来标识多个部分的时候.

我们来看看这个。 本质是:PR需要小而快!

continue reading>>
CDN, 边缘, 缓存, edge, center, cache, hit, rate, backsource, log-log, zipf

掐指算算: 你的CDN多花了几百万?

在上篇 互联网中对象访问频率的91分布 我们通过 90%的流量由10%的内容产生 这句经验描述， 得出了访问频率的zipf模型:

\[f(k) = c/k^s \tag{1}\]

CDN (Content delivery network) 就是一个典型的符合zipf分布的缓存系统: 将缓存服务部署在距离用户最近的上百个地区（CDN边缘机房）， 当用户需要访问热门内容时，只需在边缘机房读取，以此达到性能优化。

因为符合zipf模型， 所以，如果一个边缘机房的容量对全量数据的占比变化1%，会带来每年数十万元的成本变化。 一个中等规模的CDN系统，调优前后，可能会有每年几百万的成本差别。

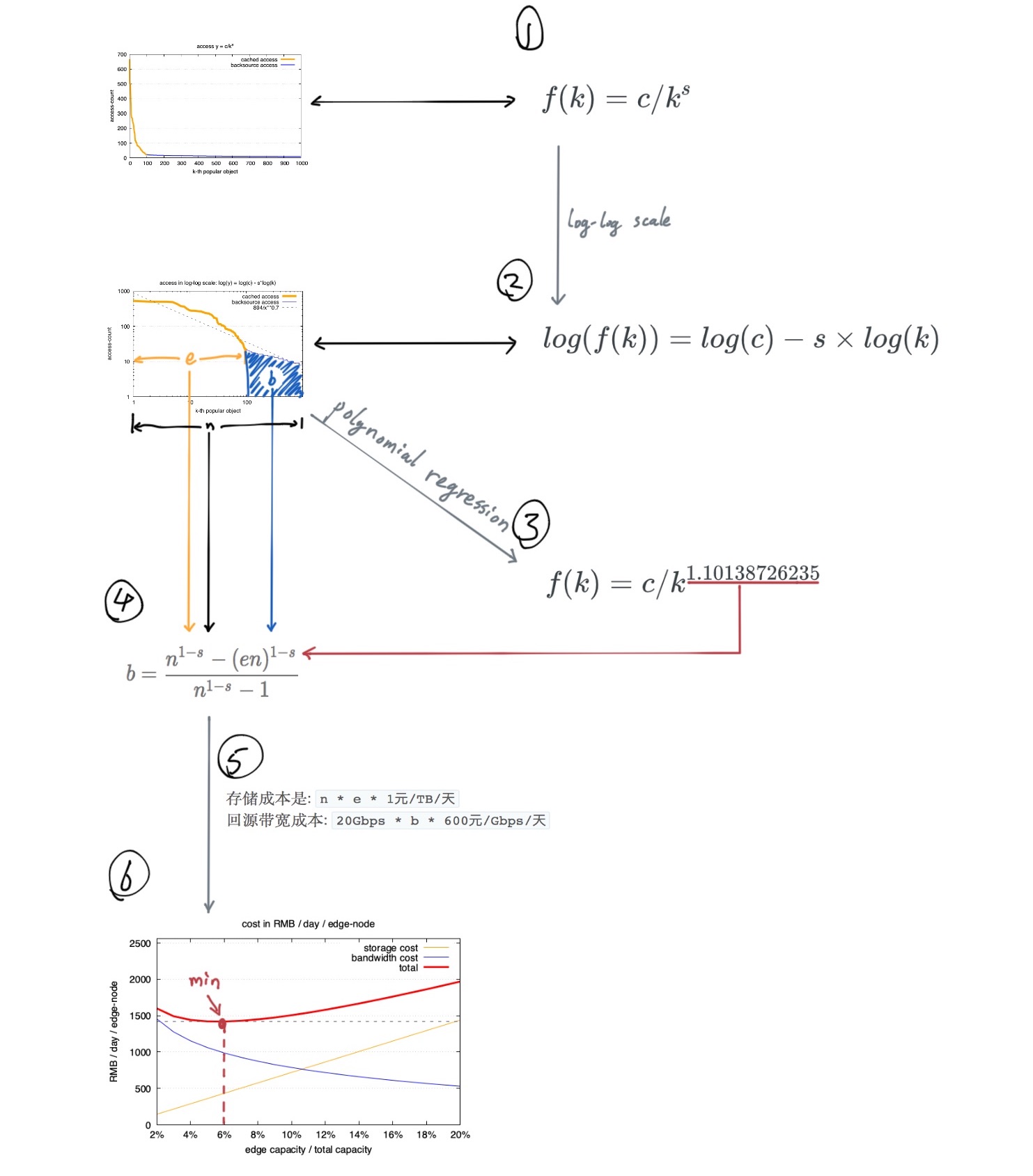
本文从原理到实践跟大家一起分析下CDN的成本构成，以及zipf如何影响成本。

本文结构:

xxx

continue reading>>
绘画

一年的素描练习

一年前, 一个偶然的机会参加了公司组织的一个成人绘画启蒙班, 突然之间想起一直都想要认真的画画, 从自己跟桌子差不多高的时候, 就喜欢画画. 无奈家长眼中自己的文化课学好了可能更不容易饿死, 于是一直没有什么机会.

这次启蒙班课程其实只有4节左右, 很快就过去了. 但从那时起, 觉得应该把这件事从人生TODOlist里开始去掉了. 于是从2018.10月开始间歇的练练, 俗话说, 一个好汉三个帮, 身边几个好友给了不少帮助. 感谢彪哥淼姐丁老, 加班之余还不忘对我指点12. 俗话又说, 一日为师, 二日为师, 日日日为师. 几个老师也被我折磨的够呛. 可以说, 对我自己的人生产生了关键的影响.

到此为止, 回头看看这一年的变化, 有些进步, 也参差不齐的摸索. 相比外在的变化带来的快乐, 看到自己自身的变化(积极的), 更能让人开心.

japenese-girl-2
2019-12-25
girl
2019-12-23
梦露
2019-11-29
japanese-girl-1
2019-11-14
碳粉
2019-10-21
fashion
2019-10-11
wz-girl
2019-09-23
临摹
2019-09-12
碳条
2019-08-31
龙妈-生活照
2019-08-28
影
2019-08-11
xxx-girl-03
2019-07-06
林媛
2019-06-26
haircut-girl
2019-06-18
石原里美
2019-06-11
black-widow
2019-05-26
影-杨平
2019-05-20
江一燕
2019-05-12
Daenerys-Targaryen
2019-04-09
xxx-girl-02
2019-03-13
xxx-girl-01
2019-03-10
赵岩
2019-02-13
马龙-白兰度
2019-02-09
影-小艾
2019-02-04
Skull
2019-02-02
Halle Berry
2019-01-26
Bumblebee girl
2019-01-13
Girl right side
2019-01-05
Tom-Hardy
2018-12-12
A Girl
2018-12-08
Breaking-Bad
2018-11-17
伽罗
2018-11-04
小龙女
2018-10-04
Morning girl
2018-10-01
continue reading>>
log-log, zipf

互联网中对象访问频率的91分布

在互联网领域, 流行着这么一句话:

90%的流量由10%的内容产生.

缓存也由此产生: 只为最频繁访问的10%的内容提供更快的存储, 就可以以很低的成本提供尽可能好的服务质量.

一般符合这种互联网访问模型的曲线是下图这样的. 对每个访问的url做独立计数, 并按照从访问最多到最低排序:

xxx

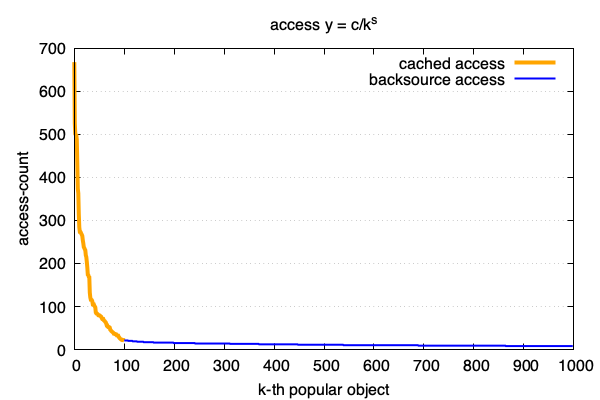
这句是一个经验结论, 从它可以得出我们的频度分布公式: 也就是zipf 模型.

\[f(k) = c/k^s\]

这个公式很好, 好就好在可以直接对其左右两边取对数后, 直接转换成了线性关系:

\[log(f(k)) = log(c) - s \times log(k)\]

即: k的对数跟y的对数呈现线性关系. 线性太棒了, 简单又好用!

xxx

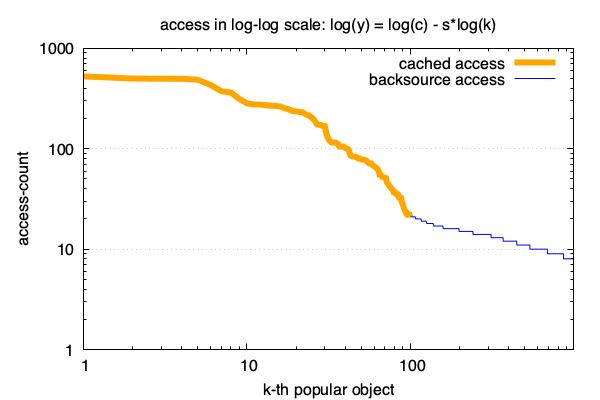
用这个公式我们可以更好的了解和控制数据的访问模型, 做更多的事情. 以下是得出这个结论的愉快的推倒过程.

continue reading>>
dictionary, 树, 有根图, recursive, interview, infinite, compare, 比较

哄好面试官系列-1: 比较2个python dict(多级)是否相同

工作面试是个很有意思的过程, 面试经常是一个对未知领域初步了解的最好时机(对双方都是), 面试官和面试人通常也会尽力在最短的时间里表达/接受尽可能多的信息.

因此面试题一般也是比较有趣的: 它浓缩了日常工作中的典型和有挑战性的问题, 而又不会带有太多日常工作中的繁琐.

在技术面试中, 要哄好面试官, 最重要的无疑是能把一个问题解释的完善严谨.

于是打算收集一些 有趣 的问题, 跟大家分享. 本次先唠唠这个:

问题: 比较2个多级dict是否相同

2个多级dict可以看成2个树的对比, 此类问题应该在刷题网站上有不少了, 似乎用树的遍历就可以了, 然而可达鸭认为事情并不简单. 在深入答案之前, 我们先明确下问题的描述:

  • 一个dict中有多个key, 每个key对应一个子dict. 为了简化问题, 假设dict中的key对应的value都是dict, 没有其他类型.

  • 如果能够用来访问a的所有的key也可以用来访问b, 就认为2个dict相同, 例如:

    a = {'foo':{'bar':{}}}; b = {'foo':{'bar':{}}} 就是一对相同的dict:

    • a['foo']和b['foo']都存在.
    • a['foo']['bar']和b['foo']['bar']也都存在.

思路: 递归

比较2个dict同构的思路很直接:

  • 对于2个dict: a 和 b, 先比较这2个dict各自的key的集合一致, 如果不一致肯定2个dict不一样.

  • 再逐个对比每个key对应的子dict是否一样. 直到遍历完所有的子dict.

def eq(a, b):

    for k in set(a) | set(b):

        if k not in a or k not in b:
            return False

        if not eq(a[k], b[k]):
            return False

    return True

print eq({}, {'x':{}}) # False
print eq({'x':{}}, {'x':{}}) # True

上面的代码差不多可以把大部分面试官哄到6成满意度.

continue reading>>
storage, minhash, similarity, compact, algorithm, constant-time, constant-space, 存储, 最小哈希, 相似性, 合并, 算法, 常量时间, 常量空间

存储中的文件合并策略优化

系统中的所有数据以block 存放, 2个block中可能包含大量的重复文件, 这时我们需要找出这2个block, 将其合并,

问题: 如何高效的(在时间上和空间上) 找出具有大量重复文件的block对.

假设:

  • 每个block的文件数 n = 1000万
  • 单个文件名长度: l = 512 字节
  • hash-bitmap 大小 64 * 10^6 = 8MB
  • min-hash bucket数量 b = 128

各种算法的开销如下

算法\开销 空间开销 实际空间 时间开销
fn-list O(n x l) 5GB O(n x l)
hash-bitmap O(n) 8MB O(n)
min-hash O(1) 1KB O(1)
continue reading>>
杂谈

软件工程是个面包机

我们平时印象中的面包机是这个样子的:

烤面包机属于加热电器。其功能是在面包片附近生成足够的热量，以便对面包进行烘烤

面包机的原理非常的简单, 有个开关控制通电, 通过电热来加热, 这些基本的原理普通的中学生都知道, 也都能在wikipedia上找到. 这么简单的东西…

如果我们要亲手制作一个面包机, 需要花费多久呢?

话说, 英国有个叫Thomas Thwaites 的艺术家, 几年前, 花了9个月的时间做了一个面包机.

恩…没错, 9个月!

如果依赖现代社会的完善体系, 这件事情是很简单的,

之所以花费了这么久, 是因为他没有使用现成的零件, 一切都是从头开始制作的!

我们看看他到底怎么完成的:

continue reading>>
杂谈

程序员必须知道的事情, 一般人我不告诉他

  • 软件开发里所有的东西都已经发明出来了! 人们总是在做重复的事情, 假装在发明新的东西. 如果有个东西让你觉得很酷很新, 那它肯定是从Smalltalk, HAKMEM, Ivan Sutherland, Douglas Engelbart, 早期的IBM, 或者Bell 实验室其中之一抄来的.
continue reading>>
cgroup, ld_preload

cgexec 无法继承 LD_PRELOAD 环境变量

continue reading>>
mysql, group, replication

mysql group replication实践记录: 步骤, 问题和注意事项

continue reading>>
math, pythagorean, 勾股数

枚举所有整勾股数

勾股数可以写成 x^2 - y^2, 2xy, x^2 + y^2 的形式, 因为 (x^2 - y^2)^2 + (2xy)^2 = (x^2 + y^2)^2

结论1: 如果x, y是互质整数, 则一组 x, y 对应一组互质整勾股数 a, b, c.

continue reading>>
ansible, devops, include, include_tasks, import_tasks

ansible中的include, include_tasks 和 import_tasks 的差别

include 被deprecated了. 建议使用include_tasks 和 import_tasks.

  • include_tasks 是动态的: 在运行时展开. when只应用一次. 被include的文件名可以使用变量.

  • import_tasks 是静态的: 在加载时展开. when在被import的文件里的每个task, 都会重新检查一次. 因为是加载时展开的, 文件名的变量不能是动态设定的.

    When using static includes, ensure that any variables used in their names are defined in vars/vars_files or extra-vars passed in from the command line. Static includes cannot use variables from inventory sources like group or host vars.

continue reading>>
python, debug, concurrency, race-condition, multithread, popen, subprocess

python 并发subprocess.Popen的坑

一个父进程里多个线程并发地调用subprocess.Popen来创建子进程的时候, 会有几率出现Popen长时间不返回的情况.

这个问题是由于fd被多个子进程同时继承导致的.

感谢评论中的 周波 的提醒:

python3.4 CentOS Linux release 7.3.1611 (Core), 默认值已经是True

这个问题只作为一个case来分享, 高版本的python不必再担心啦~

重现问题的代码

下面这个小程序启动2个线程, 每个线程各自(通过subprocess.Popen)启动一个子进程, 一个子进程执行echo 1后就直接返回; 另一个子进程启动后, sleep 0.03秒后返回.

程序里统计了2个调用Popen花的时间, 运行后可以发现, echo的进程有时启动很快(小于预期的0.01秒, 仅仅是启动, 不包括执行时间), 有时会很慢(超过0.03秒), 刚好和另一个sleep的进程执行时间吻合. 调大sleep子进程的时间可以看到echo也会同样有几率返回慢.

continue reading>>
hash, collision, math, zh

程序员必读: 摸清hash表的脾性

hash表中key的分布规律

当hash表中key和bucket数量一样时(n/b=1):

  • 37% 的桶是空的.
  • 37% 的桶里只有1个key.
  • 26% 的桶里有1个以上的key(hash冲突).

下面这个图更直观的展示了当n=b=20的时候, hash表中每个bucket中key的个数的分布, (我们按照key的数量对bucket做了排序):

continue reading>>
python, debug, memory, leak, tool

python 进程内存增长问题, 解决方法和工具

表现

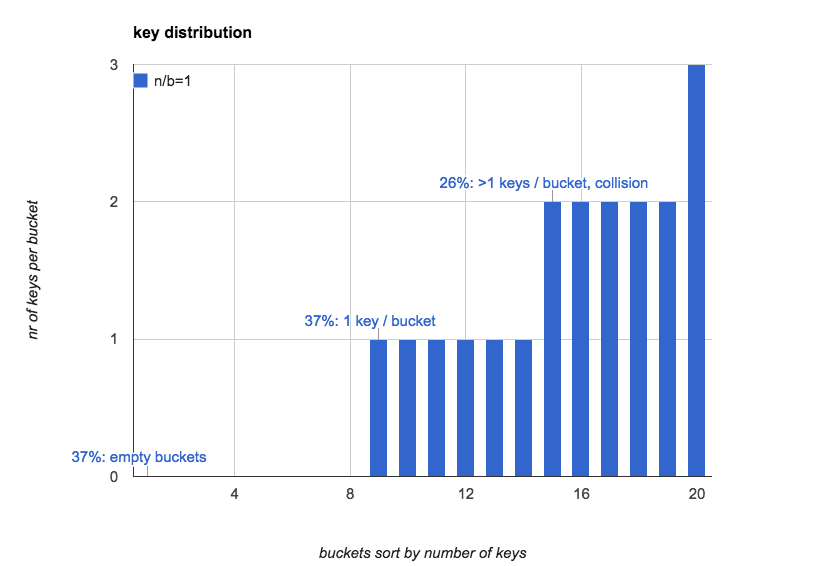
运行环境:

# uname -a
Linux ** 3.10.0-327.el7.x86_64 #1 SMP Thu Nov 19 22:10:57 UTC 2015 x86_64 x86_64 x86_64 GNU/Linux

# python2 --version
Python 2.7.5

# cat /etc/*-release
CentOS Linux release 7.2.1511 (Core)
continue reading>>
theory, distributed, tutorial, replication, erasure, code

xp的分布式系统系列教程之: Erasure-Code: 工作原理, 数学解释, 实践和分析.

文字版: Erasure-Code: 工作原理, 数学解释, 实践和分析

continue reading>>
theory, distributed, tutorial, replication, erasure, code

xp的分布式系统系列教程之: Erasure-Code: 工作原理, 数学解释, 实践和分析.

内容简介

Erasure-Code, 简称 EC, 也叫做 擦除码 或 纠删码, 指使用 范德蒙(Vandermonde) 矩阵的 里德-所罗门码(Reed-Solomon) 擦除码算法.

EC 本身是1组数据冗余和恢复的算法的统称.

本文以 Vandermonde 矩阵的 Reed-Solomon 来解释 EC 的原理.

术语定义:

  • $d_j$ 表示数据块.
  • $y_i$ 表示通过数据块计算得来的, 作为数据冗余的校验块.
  • $u_j$ 表示丢失的, 需要恢复的数据块.
  • k 表示数据块的数量.
  • m 表示校验块的数量.
continue reading>>